ಕಾಂತೀಯ ಕ್ಷೇತ್ರ ಮತ್ತು ಅದರ ನಿಯತಾಂಕಗಳು, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳು

"ಕಾಂತೀಯ ಕ್ಷೇತ್ರ" ಎಂಬ ಪದದ ಅಡಿಯಲ್ಲಿ ಕಾಂತೀಯ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಶಕ್ತಿಗಳು ವ್ಯಕ್ತವಾಗುವ ಒಂದು ನಿರ್ದಿಷ್ಟ ಶಕ್ತಿಯ ಜಾಗವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ವಾಡಿಕೆ. ಅವರು ಕಾಳಜಿ ವಹಿಸುತ್ತಾರೆ:

• ಪ್ರತ್ಯೇಕ ವಸ್ತುಗಳು: ಫೆರಿಮ್ಯಾಗ್ನೆಟ್‌ಗಳು (ಲೋಹಗಳು - ಮುಖ್ಯವಾಗಿ ಎರಕಹೊಯ್ದ ಕಬ್ಬಿಣ, ಕಬ್ಬಿಣ ಮತ್ತು ಅವುಗಳ ಮಿಶ್ರಲೋಹಗಳು) ಮತ್ತು ಅವುಗಳ ವರ್ಗದ ಫೆರೈಟ್‌ಗಳು, ರಾಜ್ಯವನ್ನು ಲೆಕ್ಕಿಸದೆ;

• ವಿದ್ಯುತ್ ಚಲಿಸುವ ಶುಲ್ಕಗಳು.

ಎಲೆಕ್ಟ್ರಾನ್ಗಳ ಸಾಮಾನ್ಯ ಕಾಂತೀಯ ಕ್ಷಣ ಅಥವಾ ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳ ಇತರ ಕಣಗಳನ್ನು ಹೊಂದಿರುವ ಭೌತಿಕ ದೇಹಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ... ಅವರ ಪರಸ್ಪರ ಕ್ರಿಯೆಯನ್ನು ಫೋಟೋದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳು.

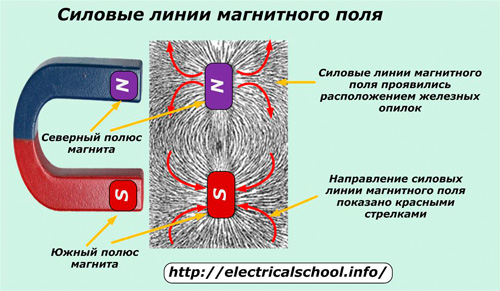
ಕಬ್ಬಿಣದ ಫೈಲಿಂಗ್‌ಗಳ ಸಮ ಪದರದೊಂದಿಗೆ ರಟ್ಟಿನ ಹಾಳೆಯ ಹಿಂಭಾಗಕ್ಕೆ ಶಾಶ್ವತ ಮ್ಯಾಗ್ನೆಟ್ ಅನ್ನು ತಂದ ನಂತರ ಅವು ರೂಪುಗೊಳ್ಳುತ್ತವೆ. ಚಿತ್ರವು ಉತ್ತರ (N) ಮತ್ತು ದಕ್ಷಿಣ (S) ಧ್ರುವಗಳ ಸ್ಪಷ್ಟ ಗುರುತುಗಳನ್ನು ಅವುಗಳ ದೃಷ್ಟಿಕೋನಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಕ್ಷೇತ್ರ ರೇಖೆಗಳ ದಿಕ್ಕಿನೊಂದಿಗೆ ತೋರಿಸುತ್ತದೆ: ಉತ್ತರ ಧ್ರುವದಿಂದ ನಿರ್ಗಮನ ಮತ್ತು ದಕ್ಷಿಣ ಧ್ರುವದ ಪ್ರವೇಶ.

ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಹೇಗೆ ರಚಿಸಲಾಗಿದೆ

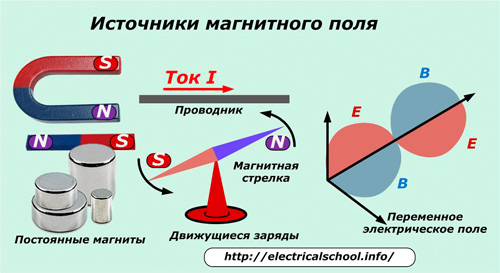
ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಮೂಲಗಳು:

• ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳು;

• ಮೊಬೈಲ್ ಶುಲ್ಕಗಳು;

• ಸಮಯ ಬದಲಾಗುವ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರ.

ಶಿಶುವಿಹಾರದ ಪ್ರತಿ ಮಗುವಿಗೆ ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳ ಕ್ರಿಯೆಯೊಂದಿಗೆ ಪರಿಚಿತವಾಗಿದೆ.ಎಲ್ಲಾ ನಂತರ, ಅವರು ಈಗಾಗಲೇ ರೆಫ್ರಿಜರೇಟರ್‌ನಲ್ಲಿ ಎಲ್ಲಾ ರೀತಿಯ ಗುಡಿಗಳ ಪ್ಯಾಕೆಟ್‌ಗಳಿಂದ ತೆಗೆದ ಚಿತ್ರಗಳು-ಆಯಸ್ಕಾಂತಗಳನ್ನು ಕೆತ್ತಿಸಬೇಕಾಗಿತ್ತು.

ಚಲನೆಯಲ್ಲಿರುವ ವಿದ್ಯುದಾವೇಶಗಳು ಸಾಮಾನ್ಯವಾಗಿ ಕಾಂತಕ್ಷೇತ್ರದ ಶಕ್ತಿಗಿಂತ ಗಮನಾರ್ಹವಾಗಿ ಹೆಚ್ಚಿನ ಶಕ್ತಿಯನ್ನು ಹೊಂದಿರುತ್ತವೆ ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳು… ಇದನ್ನು ಬಲದ ರೇಖೆಗಳಿಂದಲೂ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಪ್ರಸ್ತುತ I ನೊಂದಿಗೆ ನೇರ ತಂತಿಗಾಗಿ ಅವರ ರೇಖಾಚಿತ್ರಕ್ಕಾಗಿ ನಿಯಮಗಳನ್ನು ವಿಶ್ಲೇಷಿಸೋಣ.

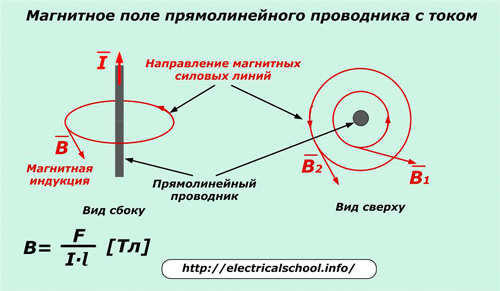
ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಯನ್ನು ಪ್ರಸ್ತುತದ ಚಲನೆಗೆ ಲಂಬವಾಗಿರುವ ಸಮತಲದಲ್ಲಿ ಎಳೆಯಲಾಗುತ್ತದೆ, ಆದ್ದರಿಂದ ಅದರ ಪ್ರತಿಯೊಂದು ಬಿಂದುಗಳಲ್ಲಿ ಕಾಂತೀಯ ಸೂಜಿಯ ಉತ್ತರ ಧ್ರುವದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವು ಈ ರೇಖೆಗೆ ಸ್ಪರ್ಶವಾಗಿ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ. ಇದು ಚಲಿಸುವ ಚಾರ್ಜ್ ಸುತ್ತಲೂ ಕೇಂದ್ರೀಕೃತ ವಲಯಗಳನ್ನು ರಚಿಸುತ್ತದೆ.

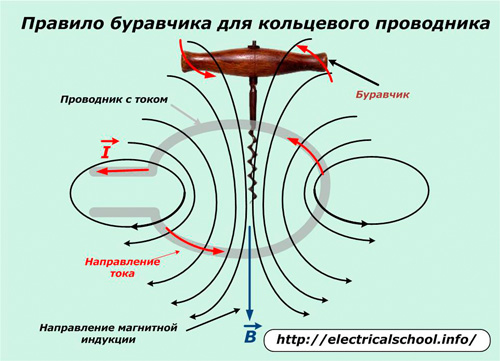
ಈ ಬಲಗಳ ದಿಕ್ಕನ್ನು ಪ್ರಸಿದ್ಧ ತಿರುಪು ಅಥವಾ ಬಲಗೈ ಸ್ಕ್ರೂ ನಿಯಮದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ಗಿಮ್ಲೆಟ್ ನಿಯಮ

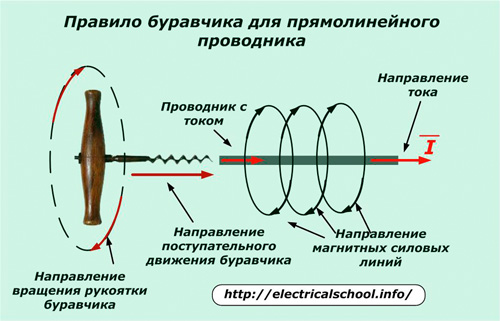
ಪ್ರಸ್ತುತ ವೆಕ್ಟರ್ನೊಂದಿಗೆ ಗಿಂಬಲ್ ಏಕಾಕ್ಷವನ್ನು ಇರಿಸಲು ಮತ್ತು ಹ್ಯಾಂಡಲ್ ಅನ್ನು ತಿರುಗಿಸಲು ಇದು ಅವಶ್ಯಕವಾಗಿದೆ, ಇದರಿಂದಾಗಿ ಗಿಂಬಲ್ನ ಮುಂದಕ್ಕೆ ಚಲನೆಯು ಅದರ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ. ನಂತರ ಹ್ಯಾಂಡಲ್ ಅನ್ನು ತಿರುಗಿಸುವ ಮೂಲಕ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳ ದೃಷ್ಟಿಕೋನವನ್ನು ಸೂಚಿಸಲಾಗುತ್ತದೆ.

ರಿಂಗ್ ಕಂಡಕ್ಟರ್‌ನಲ್ಲಿ, ಹ್ಯಾಂಡಲ್‌ನ ತಿರುಗುವಿಕೆಯ ಚಲನೆಯು ಪ್ರವಾಹದ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ ಮತ್ತು ಅನುವಾದ ಚಲನೆಯು ಇಂಡಕ್ಷನ್‌ನ ದೃಷ್ಟಿಕೋನವನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳು ಯಾವಾಗಲೂ ಉತ್ತರ ಧ್ರುವವನ್ನು ಬಿಟ್ಟು ದಕ್ಷಿಣ ಧ್ರುವವನ್ನು ಪ್ರವೇಶಿಸುತ್ತವೆ. ಅವು ಆಯಸ್ಕಾಂತದೊಳಗೆ ಮುಂದುವರಿಯುತ್ತವೆ ಮತ್ತು ಎಂದಿಗೂ ತೆರೆದುಕೊಳ್ಳುವುದಿಲ್ಲ.

ಹೆಚ್ಚಿನ ವಿವರಗಳಿಗಾಗಿ ಇಲ್ಲಿ ನೋಡಿ: ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್‌ನಲ್ಲಿ ಗಿಂಬಲ್ ನಿಯಮವು ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ

ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ನಿಯಮಗಳು

ವಿವಿಧ ಮೂಲಗಳಿಂದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳು ಪರಿಣಾಮವಾಗಿ ಕ್ಷೇತ್ರವನ್ನು ರೂಪಿಸುತ್ತವೆ.

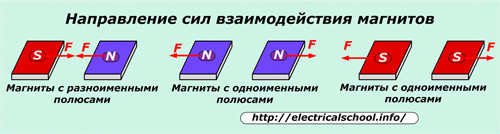
ಈ ಸಂದರ್ಭದಲ್ಲಿ, ವಿರುದ್ಧ ಧ್ರುವಗಳೊಂದಿಗೆ (N - S) ಆಯಸ್ಕಾಂತಗಳು ಪರಸ್ಪರ ಆಕರ್ಷಿತವಾಗುತ್ತವೆ ಮತ್ತು ಅದೇ ಹೆಸರುಗಳೊಂದಿಗೆ (N - N, S - S) - ಅವರು ಪರಸ್ಪರ ಹಿಮ್ಮೆಟ್ಟಿಸುತ್ತಾರೆ.ಧ್ರುವಗಳ ನಡುವಿನ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಶಕ್ತಿಗಳು ಅವುಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಧ್ರುವಗಳನ್ನು ಹತ್ತಿರಕ್ಕೆ ಸ್ಥಳಾಂತರಿಸಲಾಗುತ್ತದೆ, ಹೆಚ್ಚು ಬಲವು ಉತ್ಪತ್ತಿಯಾಗುತ್ತದೆ.

ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಮೂಲ ಗುಣಲಕ್ಷಣಗಳು

ಅವು ಸೇರಿವೆ:

• ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ (ವಿ);

• ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ (ಎಫ್);

• ಫ್ಲಕ್ಸ್ ಲಿಂಕ್ (Ψ).

ಕ್ಷೇತ್ರದ ಪ್ರಭಾವದ ತೀವ್ರತೆ ಅಥವಾ ಬಲವನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್‌ನ ಮೌಲ್ಯ ವೆಕ್ಟರ್‌ನಿಂದ ಅಂದಾಜಿಸಲಾಗಿದೆ ... ಇದು "ಎಫ್" ಬಲದ ಮೌಲ್ಯದಿಂದ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ "ನಾನು" ಉದ್ದದ ತಂತಿಯ ಮೂಲಕ ಹಾದುಹೋಗುವ ಪ್ರವಾಹದಿಂದ ರಚಿಸಲಾಗಿದೆ "ಎಲ್" ». V= F / (I ∙ l)

SI ವ್ಯವಸ್ಥೆಯಲ್ಲಿನ ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ಮಾಪನದ ಘಟಕವು ಟೆಸ್ಲಾ ಆಗಿದೆ (ಈ ವಿದ್ಯಮಾನಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಿದ ಮತ್ತು ಗಣಿತದ ವಿಧಾನಗಳನ್ನು ಬಳಸಿ ವಿವರಿಸಿದ ಭೌತಶಾಸ್ತ್ರಜ್ಞರ ನೆನಪಿಗಾಗಿ). ರಷ್ಯಾದ ತಾಂತ್ರಿಕ ಸಾಹಿತ್ಯದಲ್ಲಿ, ಇದನ್ನು "ಟಿ" ಎಂದು ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ, ಮತ್ತು ಅಂತರರಾಷ್ಟ್ರೀಯ ದಾಖಲಾತಿಯಲ್ಲಿ, "ಟಿ" ಚಿಹ್ನೆಯನ್ನು ಅಳವಡಿಸಲಾಗಿದೆ.

1 T ಎಂಬುದು ಅಂತಹ ಏಕರೂಪದ ಕಾಂತೀಯ ಹರಿವಿನ ಪ್ರಚೋದನೆಯಾಗಿದ್ದು, ಇದು 1 ಆಂಪಿಯರ್ನ ಪ್ರವಾಹವು ಆ ತಂತಿಯ ಮೂಲಕ ಹಾದುಹೋದಾಗ ಕ್ಷೇತ್ರದ ದಿಕ್ಕಿಗೆ ಲಂಬವಾಗಿರುವ ನೇರ ತಂತಿಯ ಮೇಲೆ ಪ್ರತಿ ಮೀಟರ್ ಉದ್ದಕ್ಕೆ 1 ನ್ಯೂಟನ್ ಬಲದೊಂದಿಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.

1T = 1 ∙ N / (A ∙ m)

ವೆಕ್ಟರ್ ದಿಕ್ಕು V ಎಡಗೈ ನಿಯಮದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

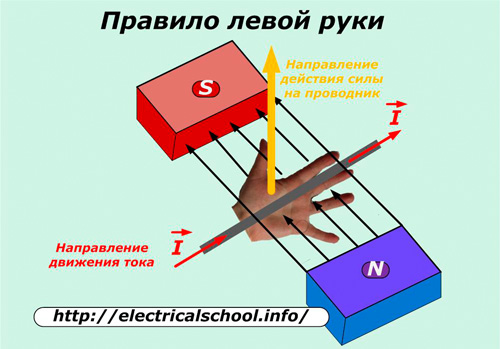
ನಿಮ್ಮ ಎಡಗೈಯ ಅಂಗೈಯನ್ನು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಿದರೆ, ಉತ್ತರ ಧ್ರುವದಿಂದ ಬಲದ ರೇಖೆಗಳು ಬಲ ಕೋನದಲ್ಲಿ ಅಂಗೈಯನ್ನು ಪ್ರವೇಶಿಸಿ ಮತ್ತು ತಂತಿಯಲ್ಲಿನ ಪ್ರವಾಹದ ದಿಕ್ಕಿನಲ್ಲಿ ನಾಲ್ಕು ಬೆರಳುಗಳನ್ನು ಇರಿಸಿ, ನಂತರ ಚಾಚಿಕೊಂಡಿರುವ ಹೆಬ್ಬೆರಳು ಸೂಚಿಸುತ್ತದೆ ಆ ತಂತಿಯ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲದ ದಿಕ್ಕು.

ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ಹೊಂದಿರುವ ವಾಹಕವು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳಿಗೆ ಲಂಬ ಕೋನಗಳಲ್ಲಿ ಇಲ್ಲದಿದ್ದಲ್ಲಿ, ಅದರ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವು ಪ್ರಸ್ತುತ ಹರಿಯುವ ಮೌಲ್ಯ ಮತ್ತು ವಾಹಕದ ಉದ್ದದ ಪ್ರಕ್ಷೇಪಣದ ಅಂಶಕ್ಕೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. ಲಂಬ ದಿಕ್ಕಿನಲ್ಲಿ ನೆಲೆಗೊಂಡಿರುವ ಸಮತಲದಲ್ಲಿ ಪ್ರಸ್ತುತ.

ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವು ವಾಹಕವನ್ನು ತಯಾರಿಸಿದ ವಸ್ತುಗಳ ಮೇಲೆ ಮತ್ತು ಅದರ ಅಡ್ಡ-ವಿಭಾಗದ ಪ್ರದೇಶವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ. ಈ ತಂತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲದಿದ್ದರೂ ಮತ್ತು ಚಲಿಸುವ ಶುಲ್ಕಗಳು ಕಾಂತೀಯ ಧ್ರುವಗಳ ನಡುವೆ ವಿಭಿನ್ನ ಪರಿಸರದಲ್ಲಿ ಚಲಿಸಲು ಪ್ರಾರಂಭಿಸಿದರೂ, ಈ ಬಲವು ಯಾವುದೇ ರೀತಿಯಲ್ಲಿ ಬದಲಾಗುವುದಿಲ್ಲ.

ಕಾಂತಕ್ಷೇತ್ರದ ಒಳಗೆ ಎಲ್ಲಾ ಬಿಂದುಗಳಲ್ಲಿ ವೆಕ್ಟರ್ V ಒಂದೇ ದಿಕ್ಕು ಮತ್ತು ಪ್ರಮಾಣವನ್ನು ಹೊಂದಿದ್ದರೆ, ಅಂತಹ ಕ್ಷೇತ್ರವನ್ನು ಏಕರೂಪವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ.

ಯಾವುದೇ ಪರಿಸರದೊಂದಿಗೆ ಕಾಂತೀಯ ಗುಣಲಕ್ಷಣಗಳು, ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ ವಿ ಮೌಲ್ಯದ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ (ಎಫ್)

ಒಂದು ನಿರ್ದಿಷ್ಟ ಪ್ರದೇಶದ ಮೂಲಕ ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ಅಂಗೀಕಾರವನ್ನು ನಾವು ಪರಿಗಣಿಸಿದರೆ S, ನಂತರ ಅದರ ಗಡಿಗಳಿಗೆ ಸೀಮಿತವಾದ ಇಂಡಕ್ಷನ್ ಅನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

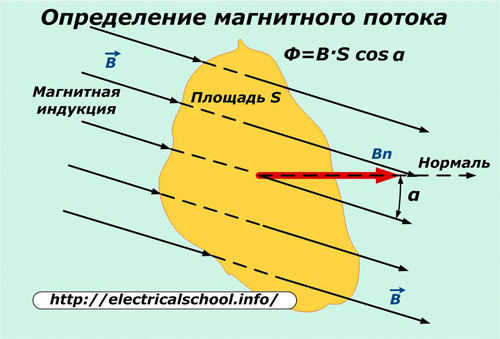
ಆಯಸ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ದಿಕ್ಕಿಗೆ ಕೆಲವು ಕೋನ α ನಲ್ಲಿ ಪ್ರದೇಶವು ಒಲವನ್ನು ಹೊಂದಿರುವಾಗ, ಪ್ರದೇಶದ ಇಳಿಜಾರಿನ ಕೋನದ ಕೊಸೈನ್‌ನೊಂದಿಗೆ ಕಾಂತೀಯ ಹರಿವು ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಪ್ರದೇಶವು ಅದರ ನುಗ್ಗುವ ಇಂಡಕ್ಷನ್ಗೆ ಲಂಬವಾಗಿರುವಾಗ ಅದರ ಗರಿಷ್ಠ ಮೌಲ್ಯವನ್ನು ರಚಿಸಲಾಗುತ್ತದೆ. Ф = ವಿ ಎಸ್

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನ ಮಾಪನದ ಘಟಕವು 1 ವೆಬರ್ ಆಗಿದೆ, ಇದು 1 ಚದರ ಮೀಟರ್ ಪ್ರದೇಶದ ಮೂಲಕ 1 ಟೆಸ್ಲಾವನ್ನು ಇಂಡಕ್ಷನ್ ಮೂಲಕ ನಿರ್ಧರಿಸುತ್ತದೆ.

ಸ್ಟ್ರೀಮಿಂಗ್ ಸಂಪರ್ಕ

ಆಯಸ್ಕಾಂತದ ಧ್ರುವಗಳ ನಡುವೆ ಇರುವ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ಪ್ರಸ್ತುತ ವಾಹಕಗಳಿಂದ ಉತ್ಪತ್ತಿಯಾಗುವ ಒಟ್ಟು ಪ್ರಮಾಣದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ಪಡೆಯಲು ಈ ಪದವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.

n ತಿರುವುಗಳ ಸಂಖ್ಯೆಯೊಂದಿಗೆ ಅದೇ ಪ್ರವಾಹವು ಸುರುಳಿಯ ಅಂಕುಡೊಂಕಾದ ಮೂಲಕ ಹಾದುಹೋದಾಗ, ಎಲ್ಲಾ ತಿರುವುಗಳ ಒಟ್ಟು (ಸಂಪರ್ಕಿತ) ಕಾಂತೀಯ ಹರಿವನ್ನು ಫ್ಲಕ್ಸ್ ಲಿಂಕೇಜ್ Ψ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

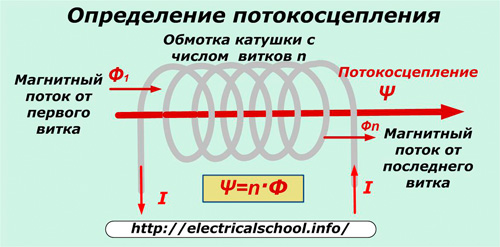
Ψ = n Ф… ಹರಿವಿನ ಅಳತೆಯ ಘಟಕವು 1 ವೆಬರ್ ಆಗಿದೆ.

ಪರ್ಯಾಯ ವಿದ್ಯುತ್‌ನಿಂದ ಕಾಂತಕ್ಷೇತ್ರವು ಹೇಗೆ ರೂಪುಗೊಳ್ಳುತ್ತದೆ

ಕಾಂತೀಯ ಕ್ಷಣಗಳೊಂದಿಗೆ ವಿದ್ಯುತ್ ಶುಲ್ಕಗಳು ಮತ್ತು ದೇಹಗಳೊಂದಿಗೆ ಸಂವಹನ ನಡೆಸುವ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಎರಡು ಕ್ಷೇತ್ರಗಳ ಸಂಯೋಜನೆಯಾಗಿದೆ:

• ವಿದ್ಯುತ್;

• ಕಾಂತೀಯ.

ಅವು ಪರಸ್ಪರ ಸಂಬಂಧ ಹೊಂದಿವೆ, ಅವು ಪರಸ್ಪರ ಸಂಯೋಜನೆಯಾಗಿದ್ದು, ಕಾಲಾನಂತರದಲ್ಲಿ ಒಂದು ಬದಲಾದಾಗ, ಇನ್ನೊಂದರಲ್ಲಿ ಕೆಲವು ವಿಚಲನಗಳು ಸಂಭವಿಸುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಮೂರು-ಹಂತದ ಜನರೇಟರ್ನಲ್ಲಿ ಪರ್ಯಾಯ ಸೈನುಸೈಡಲ್ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವನ್ನು ರಚಿಸುವಾಗ, ಅದೇ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಒಂದೇ ರೀತಿಯ ಪರ್ಯಾಯ ಹಾರ್ಮೋನಿಕ್ಸ್ನ ಗುಣಲಕ್ಷಣಗಳೊಂದಿಗೆ ಏಕಕಾಲದಲ್ಲಿ ರೂಪುಗೊಳ್ಳುತ್ತದೆ.

ವಸ್ತುಗಳ ಕಾಂತೀಯ ಗುಣಲಕ್ಷಣಗಳು

ಬಾಹ್ಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದೊಂದಿಗಿನ ಪರಸ್ಪರ ಕ್ರಿಯೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ, ವಸ್ತುಗಳನ್ನು ವಿಂಗಡಿಸಲಾಗಿದೆ:

• ಸಮತೋಲಿತ ಕಾಂತೀಯ ಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುವ ಆಂಟಿಫೆರೋಮ್ಯಾಗ್ನೆಟ್‌ಗಳು, ಈ ಕಾರಣದಿಂದಾಗಿ ದೇಹದ ಕಾಂತೀಯೀಕರಣದ ಒಂದು ಸಣ್ಣ ಮಟ್ಟವನ್ನು ರಚಿಸಲಾಗುತ್ತದೆ;

• ಬಾಹ್ಯ ಒಂದರ ಕ್ರಿಯೆಯ ವಿರುದ್ಧ ಆಂತರಿಕ ಕ್ಷೇತ್ರವನ್ನು ಕಾಂತೀಯಗೊಳಿಸುವ ಆಸ್ತಿಯೊಂದಿಗೆ diamagnets. ಬಾಹ್ಯ ಕ್ಷೇತ್ರವಿಲ್ಲದಿದ್ದಾಗ, ಅವುಗಳ ಕಾಂತೀಯ ಗುಣಲಕ್ಷಣಗಳು ಪ್ರಕಟವಾಗುವುದಿಲ್ಲ;

• ಬಾಹ್ಯ ಕ್ರಿಯೆಯ ದಿಕ್ಕಿನಲ್ಲಿ ಆಂತರಿಕ ಕ್ಷೇತ್ರವನ್ನು ಕಾಂತೀಯಗೊಳಿಸುವ ಗುಣಲಕ್ಷಣಗಳೊಂದಿಗೆ ಪ್ಯಾರಾಮ್ಯಾಗ್ನೆಟ್ಗಳು, ಇದು ಸಣ್ಣ ಪದವಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ ಕಾಂತೀಯತೆ;

• ಕ್ಯೂರಿ ಪಾಯಿಂಟ್‌ಗಿಂತ ಕೆಳಗಿನ ತಾಪಮಾನದಲ್ಲಿ ಅನ್ವಯಿಕ ಬಾಹ್ಯ ಕ್ಷೇತ್ರವಿಲ್ಲದೆ ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ಗುಣಲಕ್ಷಣಗಳು;

• ಪರಿಮಾಣ ಮತ್ತು ದಿಕ್ಕಿನಲ್ಲಿ ಅಸಮತೋಲಿತ ಕಾಂತೀಯ ಕ್ಷಣಗಳನ್ನು ಹೊಂದಿರುವ ಫೆರಿಮ್ಯಾಗ್ನೆಟ್ಗಳು.

ವಸ್ತುಗಳ ಈ ಎಲ್ಲಾ ಗುಣಲಕ್ಷಣಗಳು ಆಧುನಿಕ ತಂತ್ರಜ್ಞಾನಗಳಲ್ಲಿ ವಿವಿಧ ಅನ್ವಯಿಕೆಗಳನ್ನು ಕಂಡುಕೊಂಡಿವೆ.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳು

ಈ ಪದವನ್ನು ವಿವಿಧ ಕಾಂತೀಯ ವಸ್ತುಗಳ ಒಂದು ಸೆಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದರ ಮೂಲಕ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಹಾದುಹೋಗುತ್ತದೆ, ಅವು ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ಗಳಿಗೆ ಹೋಲುತ್ತವೆ ಮತ್ತು ಅನುಗುಣವಾದ ಗಣಿತದ ನಿಯಮಗಳಿಂದ ವಿವರಿಸಲಾಗುತ್ತದೆ (ಒಟ್ಟು ವಿದ್ಯುತ್, ಓಮ್, ಕಿರ್ಚಾಫ್, ಇತ್ಯಾದಿ.). ನೋಡು - ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್‌ನ ಮೂಲ ನಿಯಮಗಳು.

ಆಧಾರಿತ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಲೆಕ್ಕಾಚಾರಗಳು ಎಲ್ಲಾ ಟ್ರಾನ್ಸ್‌ಫಾರ್ಮರ್‌ಗಳು, ಇಂಡಕ್ಟರ್‌ಗಳು, ವಿದ್ಯುತ್ ಯಂತ್ರಗಳು ಮತ್ತು ಇತರ ಹಲವು ಸಾಧನಗಳು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿವೆ.

ಉದಾಹರಣೆಗೆ, ಕೆಲಸ ಮಾಡುವ ವಿದ್ಯುತ್ಕಾಂತದಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ಸ್ಟೀಲ್ಸ್ ಮತ್ತು ಗಾಳಿಯಿಂದ ಮಾಡಲ್ಪಟ್ಟ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ. ಈ ಅಂಶಗಳ ಸಂಯೋಜನೆಯು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ರೂಪಿಸುತ್ತದೆ.

ಹೆಚ್ಚಿನ ವಿದ್ಯುತ್ ಸಾಧನಗಳು ತಮ್ಮ ವಿನ್ಯಾಸದಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳನ್ನು ಹೊಂದಿವೆ. ಈ ಲೇಖನದಲ್ಲಿ ಅದರ ಬಗ್ಗೆ ಇನ್ನಷ್ಟು ಓದಿ - ವಿದ್ಯುತ್ ಸಾಧನಗಳ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳು

ಈ ವಿಷಯದ ಬಗ್ಗೆ ಸಹ ಓದಿ: ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಲೆಕ್ಕಾಚಾರಗಳ ಉದಾಹರಣೆಗಳು