ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು, ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ಪ್ರಸರಣ

1864 ರಲ್ಲಿ, ಜೇಮ್ಸ್ ಕ್ಲರ್ಕ್ ಮ್ಯಾಕ್ಸ್ವೆಲ್ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ಸಾಧ್ಯತೆಯನ್ನು ಊಹಿಸಿದರು. ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯತೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಆ ಸಮಯದಲ್ಲಿ ತಿಳಿದಿರುವ ಎಲ್ಲಾ ಪ್ರಾಯೋಗಿಕ ದತ್ತಾಂಶಗಳ ವಿಶ್ಲೇಷಣೆಯಿಂದ ಪಡೆದ ತೀರ್ಮಾನಗಳ ಆಧಾರದ ಮೇಲೆ ಅವರು ಈ ಹಕ್ಕು ಮಂಡಿಸಿದರು.

ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್ ನಿಯಮಗಳನ್ನು ಗಣಿತಶಾಸ್ತ್ರೀಯವಾಗಿ ಸಂಯೋಜಿಸಿದರು, ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯ ವಿದ್ಯಮಾನಗಳನ್ನು ಸಂಪರ್ಕಿಸುತ್ತಾರೆ ಮತ್ತು ಹೀಗೆ ಸಮಯದೊಂದಿಗೆ ಬದಲಾಗುವ ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳು ಪರಸ್ಪರ ಉತ್ಪತ್ತಿಯಾಗುತ್ತವೆ ಎಂಬ ತೀರ್ಮಾನಕ್ಕೆ ಬಂದರು.

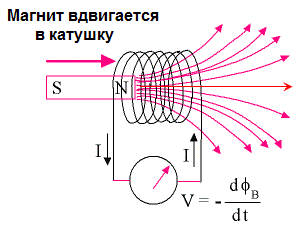
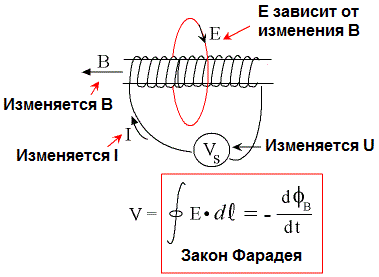
ಆರಂಭದಲ್ಲಿ, ಅವರು ಕಾಂತೀಯ ಮತ್ತು ವಿದ್ಯುತ್ ವಿದ್ಯಮಾನಗಳ ನಡುವಿನ ಸಂಬಂಧವು ಸಮ್ಮಿತೀಯವಾಗಿಲ್ಲ ಎಂಬ ಅಂಶವನ್ನು ಒತ್ತಿಹೇಳಿದರು ಮತ್ತು "ಎಡ್ಡಿ ಎಲೆಕ್ಟ್ರಿಕ್ ಫೀಲ್ಡ್" ಎಂಬ ಪದವನ್ನು ಪರಿಚಯಿಸಿದರು, ಫ್ಯಾರಡೆ ಕಂಡುಹಿಡಿದ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವಿದ್ಯಮಾನದ ತನ್ನದೇ ಆದ, ನಿಜವಾದ ಹೊಸ ವಿವರಣೆಯನ್ನು ನೀಡಿದರು: "ಕಾಂತೀಯ ಪ್ರತಿ ಬದಲಾವಣೆ ಕ್ಷೇತ್ರವು ಸುತ್ತಲಿನ ಜಾಗದಲ್ಲಿ ಸುಳಿಯ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಗೋಚರಿಸುವಿಕೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ ಮತ್ತು ಬಲದ ಮುಚ್ಚಿದ ರೇಖೆಗಳೊಂದಿಗೆ.

ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಪ್ರಕಾರ, "ಬದಲಾಯಿಸುವ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ಸುತ್ತಮುತ್ತಲಿನ ಜಾಗದಲ್ಲಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ" ಎಂಬ ವಿರುದ್ಧವಾದ ಹೇಳಿಕೆಯು ಸಹ ನಿಜವಾಗಿದೆ, ಆದರೆ ಈ ಹೇಳಿಕೆಯು ಆರಂಭದಲ್ಲಿ ಕೇವಲ ಊಹೆಯಾಗಿ ಉಳಿದಿದೆ.

ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಕಾಂತೀಯ ಮತ್ತು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರಗಳ ಪರಸ್ಪರ ರೂಪಾಂತರಗಳ ನಿಯಮಗಳನ್ನು ಸ್ಥಿರವಾಗಿ ವಿವರಿಸುವ ಗಣಿತದ ಸಮೀಕರಣಗಳ ವ್ಯವಸ್ಥೆಯನ್ನು ಬರೆದರು, ಈ ಸಮೀಕರಣಗಳು ನಂತರ ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್‌ನ ಮೂಲ ಸಮೀಕರಣಗಳಾಗಿ ಮಾರ್ಪಟ್ಟವು ಮತ್ತು ಮಹಾನ್ ವಿಜ್ಞಾನಿಗಳ ಗೌರವಾರ್ಥವಾಗಿ "ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಸಮೀಕರಣಗಳು" ಎಂದು ಕರೆಯಲು ಪ್ರಾರಂಭಿಸಿದವು. ಅವುಗಳನ್ನು ಕೆಳಗೆ. ಲಿಖಿತ ಸಮೀಕರಣಗಳ ಆಧಾರದ ಮೇಲೆ ಮ್ಯಾಕ್ಸ್‌ವೆಲ್‌ನ ಕಲ್ಪನೆಯು ವಿಜ್ಞಾನ ಮತ್ತು ತಂತ್ರಜ್ಞಾನಕ್ಕೆ ಬಹಳ ಮುಖ್ಯವಾದ ಹಲವಾರು ತೀರ್ಮಾನಗಳನ್ನು ಹೊಂದಿದೆ, ಇವುಗಳನ್ನು ಕೆಳಗೆ ಪ್ರಸ್ತುತಪಡಿಸಲಾಗಿದೆ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿವೆ

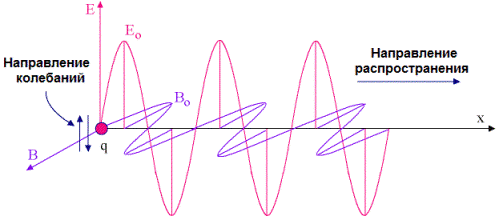
ಟ್ರಾನ್ಸ್ವರ್ಸ್ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಕಾಲಾನಂತರದಲ್ಲಿ ಹರಡುವ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಅಸ್ತಿತ್ವದಲ್ಲಿರಬಹುದು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರ… ಅಲೆಗಳು ವ್ಯತಿರಿಕ್ತವಾಗಿವೆ ಎಂಬ ಅಂಶವು ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ B ಮತ್ತು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ E ಯ ವಾಹಕಗಳು ಪರಸ್ಪರ ಲಂಬವಾಗಿರುತ್ತವೆ ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದ ಪ್ರಸರಣದ ದಿಕ್ಕಿಗೆ ಲಂಬವಾಗಿರುವ ಸಮತಲದಲ್ಲಿ ಎರಡೂ ಇರುತ್ತದೆ ಎಂಬ ಅಂಶದಿಂದ ತೋರಿಸಲಾಗಿದೆ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಸೀಮಿತ ವೇಗದಲ್ಲಿ ಹರಡುತ್ತವೆ

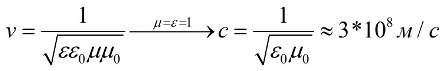
ನಿರ್ದಿಷ್ಟ ವಸ್ತುವಿನಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ಪ್ರಸರಣದ ವೇಗವು ಸೀಮಿತವಾಗಿದೆ ಮತ್ತು ತರಂಗವು ಹರಡುವ ವಸ್ತುವಿನ ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯ ಗುಣಲಕ್ಷಣಗಳಿಂದ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಸೈನುಸೈಡಲ್ ತರಂಗ λ ನ ಉದ್ದವು ನಿರ್ದಿಷ್ಟ ನಿಖರವಾದ ಅನುಪಾತದೊಂದಿಗೆ υ ವೇಗಕ್ಕೆ ಸಂಬಂಧಿಸಿದೆ λ = υ / f ಮತ್ತು ಕ್ಷೇತ್ರದ ಆಂದೋಲನಗಳ ಆವರ್ತನ ಎಫ್ ಅನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ನಿರ್ವಾತದಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದ ವೇಗ c ಮೂಲಭೂತ ಭೌತಿಕ ಸ್ಥಿರಾಂಕಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ - ನಿರ್ವಾತದಲ್ಲಿ ಬೆಳಕಿನ ವೇಗ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದ ಪ್ರಸರಣದ ವೇಗವು ಸೀಮಿತವಾಗಿದೆ ಎಂದು ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಹೇಳಿದ್ದರಿಂದ, ಇದು ಅವರ ಊಹೆ ಮತ್ತು ಆ ಸಮಯದಲ್ಲಿ ಅಂಗೀಕರಿಸಲ್ಪಟ್ಟ ದೂರದ ಕ್ರಿಯೆಯ ಸಿದ್ಧಾಂತದ ನಡುವಿನ ವಿರೋಧಾಭಾಸವನ್ನು ಸೃಷ್ಟಿಸಿತು, ಅದರ ಪ್ರಕಾರ ಅಲೆಗಳ ಪ್ರಸರಣದ ವೇಗವು ಅನಂತವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ, ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ಸಿದ್ಧಾಂತವನ್ನು ಅಲ್ಪಾವಧಿಯ ಕ್ರಿಯೆಯ ಸಿದ್ಧಾಂತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗವು ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವಾಗಿದ್ದು ಅದು ಪರಸ್ಪರ ರೂಪಾಂತರಗೊಳ್ಳುತ್ತದೆ.

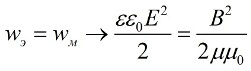
ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದಲ್ಲಿ, ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳ ರೂಪಾಂತರವು ಒಂದೇ ಸಮಯದಲ್ಲಿ ಸಂಭವಿಸುತ್ತದೆ, ಆದ್ದರಿಂದ ಕಾಂತೀಯ ಮತ್ತು ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಪರಿಮಾಣ ಸಾಂದ್ರತೆಗಳು ಪರಸ್ಪರ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ, ಇದು ನಿಜವಾಗಿದೆ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ ಈ ಕೆಳಗಿನ ಸಂಪರ್ಕದ ಮೂಲಕ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಯಾವುದೇ ಹಂತದಲ್ಲಿ ಪರಸ್ಪರ ಸಂಬಂಧ ಹೊಂದಿದೆ:

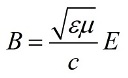
ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಶಕ್ತಿಯನ್ನು ಒಯ್ಯುತ್ತವೆ

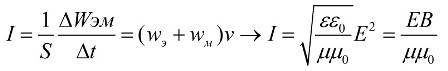
ಅದರ ಪ್ರಸರಣದ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗವು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯ ಹರಿವನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ ಮತ್ತು ತರಂಗದ ಪ್ರಸರಣದ ದಿಕ್ಕಿಗೆ ಲಂಬವಾಗಿರುವ ಸಮತಲದಲ್ಲಿನ ಪ್ರದೇಶವನ್ನು ನಾವು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡರೆ, ಒಂದು ನಿರ್ದಿಷ್ಟ ಪ್ರಮಾಣದ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯು ಅದರ ಮೂಲಕ ಚಲಿಸುತ್ತದೆ. ಕಡಿಮೆ ಸಮಯ. ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯ ಹರಿವಿನ ಸಾಂದ್ರತೆಯು ಒಂದು ಯುನಿಟ್ ಸಮಯಕ್ಕೆ ಪ್ರತಿ ಯುನಿಟ್ ಪ್ರದೇಶಕ್ಕೆ ಮೇಲ್ಮೈಯಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದಿಂದ ಸಾಗಿಸುವ ಶಕ್ತಿಯ ಪ್ರಮಾಣವಾಗಿದೆ. ವೇಗದ ಮೌಲ್ಯಗಳನ್ನು, ಹಾಗೆಯೇ ಕಾಂತೀಯ ಮತ್ತು ವಿದ್ಯುತ್ ಶಕ್ತಿಗಳನ್ನು ಬದಲಿಸುವ ಮೂಲಕ, E ಮತ್ತು B ಪ್ರಮಾಣಗಳ ಪ್ರಕಾರ ಫ್ಲಕ್ಸ್ ಸಾಂದ್ರತೆಯ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಪಡೆಯಲು ಸಾಧ್ಯವಿದೆ.

ಪಾಯಿಂಟಿಂಗ್ ವೆಕ್ಟರ್ - ಅಲೆಯ ಶಕ್ತಿಯ ಹರಿವಿನ ವೆಕ್ಟರ್

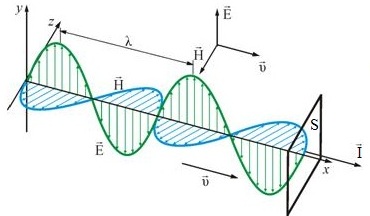
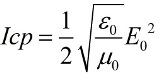
ತರಂಗ ಶಕ್ತಿಯ ಪ್ರಸರಣದ ದಿಕ್ಕು ತರಂಗದ ಪ್ರಸರಣದ ವೇಗದ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುವುದರಿಂದ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದಲ್ಲಿ ಹರಡುವ ಶಕ್ತಿಯ ಹರಿವನ್ನು ತರಂಗದ ಪ್ರಸರಣದ ವೇಗದ ರೀತಿಯಲ್ಲಿ ನಿರ್ದೇಶಿಸಿದ ವೆಕ್ಟರ್ ಬಳಸಿ ಹೊಂದಿಸಬಹುದು. ಈ ವೆಕ್ಟರ್ ಅನ್ನು "ಪಾಯಿಂಟಿಂಗ್ ವೆಕ್ಟರ್" ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ - 1884 ರಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ಹರಿವಿನ ಪ್ರಸರಣದ ಸಿದ್ಧಾಂತವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದ ಬ್ರಿಟಿಷ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಹೆನ್ರಿ ಪೊಯಿಂಟಿಂಗ್ ಅವರ ಗೌರವಾರ್ಥವಾಗಿ. ವೇವ್ ಎನರ್ಜಿ ಫ್ಲಕ್ಸ್ ಸಾಂದ್ರತೆಯನ್ನು W/m2 ನಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಅವುಗಳನ್ನು ಪ್ರತಿಬಿಂಬಿಸುವ ಅಥವಾ ಹೀರಿಕೊಳ್ಳುವ ಕಾಯಗಳ ವಿರುದ್ಧ ಒತ್ತುತ್ತವೆ

ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ವಸ್ತುವಿನ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸಿದಾಗ, ಅದರಲ್ಲಿ ಸಣ್ಣ ಪ್ರವಾಹಗಳು ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತವೆ, ಇದು ವಿದ್ಯುದಾವೇಶದ ಕಣಗಳ ಆದೇಶದ ಚಲನೆಯಾಗಿದೆ. ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಈ ಪ್ರವಾಹಗಳು ಆಂಪಿಯರ್ ಬಲದ ಕ್ರಿಯೆಗೆ ಒಳಗಾಗುತ್ತವೆ, ಇದು ವಸ್ತುವಿನೊಳಗೆ ಆಳವಾಗಿ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ. ಪರಿಣಾಮವಾಗಿ, ಆಂಪಿಯರ್ನ ಬಲವು ಒತ್ತಡವನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ.

ಈ ವಿದ್ಯಮಾನವನ್ನು ನಂತರ, 1900 ರಲ್ಲಿ, ರಷ್ಯಾದ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಪಯೋಟರ್ ನಿಕೊಲಾಯೆವಿಚ್ ಲೆಬೆಡೆವ್ ಅವರು ಪ್ರಾಯೋಗಿಕವಾಗಿ ತನಿಖೆ ಮಾಡಿದರು ಮತ್ತು ದೃಢಪಡಿಸಿದರು, ಅವರ ಪ್ರಾಯೋಗಿಕ ಕೆಲಸವು ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಸಿದ್ಧಾಂತವನ್ನು ಮತ್ತು ಭವಿಷ್ಯದಲ್ಲಿ ಅದರ ಸ್ವೀಕಾರ ಮತ್ತು ಅನುಮೋದನೆಯನ್ನು ದೃಢೀಕರಿಸುವಲ್ಲಿ ಬಹಳ ಮುಖ್ಯವಾಗಿತ್ತು.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗವು ಒತ್ತಡವನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ ಎಂಬ ಅಂಶವು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಯಾಂತ್ರಿಕ ಪ್ರಚೋದನೆಯ ಉಪಸ್ಥಿತಿಯನ್ನು ಅಂದಾಜು ಮಾಡಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ, ಇದು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯ ಪರಿಮಾಣದ ಸಾಂದ್ರತೆ ಮತ್ತು ನಿರ್ವಾತದಲ್ಲಿ ಅಲೆಯ ಪ್ರಸರಣದ ವೇಗದಿಂದ ಪ್ರತಿ ಘಟಕದ ಪರಿಮಾಣಕ್ಕೆ ವ್ಯಕ್ತಪಡಿಸಬಹುದು:

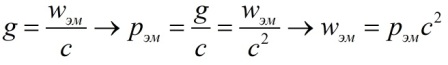
ಆವೇಗವು ದ್ರವ್ಯರಾಶಿಯ ಚಲನೆಗೆ ಸಂಬಂಧಿಸಿರುವುದರಿಂದ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ದ್ರವ್ಯರಾಶಿಯಂತಹ ಪರಿಕಲ್ಪನೆಯನ್ನು ಪರಿಚಯಿಸಲು ಸಾಧ್ಯವಿದೆ, ಮತ್ತು ನಂತರ ಒಂದು ಘಟಕದ ಪರಿಮಾಣಕ್ಕೆ ಈ ಅನುಪಾತವು (ಎಸ್ಟಿಆರ್ಗೆ ಅನುಗುಣವಾಗಿ) ಪ್ರಕೃತಿಯ ಸಾರ್ವತ್ರಿಕ ನಿಯಮದ ಸ್ವರೂಪವನ್ನು ಪಡೆದುಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಮಾನ್ಯವಾಗಿರುತ್ತದೆ. ವಸ್ತುವಿನ ರೂಪವನ್ನು ಲೆಕ್ಕಿಸದೆ ಯಾವುದೇ ವಸ್ತು ದೇಹಗಳಿಗೆ. ನಂತರ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ವಸ್ತುವಿನ ದೇಹಕ್ಕೆ ಹೋಲುತ್ತದೆ - ಇದು ಶಕ್ತಿ W, ದ್ರವ್ಯರಾಶಿ m, ಆವೇಗ p ಮತ್ತು ಟರ್ಮಿನಲ್ ವೇಗ v. ಅಂದರೆ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಪ್ರಕೃತಿಯಲ್ಲಿ ನಿಜವಾಗಿ ಅಸ್ತಿತ್ವದಲ್ಲಿರುವ ವಸ್ತುವಿನ ರೂಪಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ.

ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ಸಿದ್ಧಾಂತದ ಅಂತಿಮ ದೃಢೀಕರಣ

1888 ರಲ್ಲಿ ಮೊದಲ ಬಾರಿಗೆ, ಹೆನ್ರಿಕ್ ಹರ್ಟ್ಜ್ ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಸಿದ್ಧಾಂತವನ್ನು ಪ್ರಾಯೋಗಿಕವಾಗಿ ದೃಢಪಡಿಸಿದರು. ಅವರು ಪ್ರಾಯೋಗಿಕವಾಗಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ವಾಸ್ತವತೆಯನ್ನು ಸಾಬೀತುಪಡಿಸಿದರು ಮತ್ತು ವಿವಿಧ ಮಾಧ್ಯಮಗಳಲ್ಲಿ ವಕ್ರೀಭವನ ಮತ್ತು ಹೀರಿಕೊಳ್ಳುವಿಕೆಯಂತಹ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಿದರು, ಜೊತೆಗೆ ಲೋಹದ ಮೇಲ್ಮೈಗಳಿಂದ ಅಲೆಗಳ ಪ್ರತಿಫಲನವನ್ನು ಅಧ್ಯಯನ ಮಾಡಿದರು.

ಹರ್ಟ್ಜ್ ತರಂಗಾಂತರವನ್ನು ಅಳೆಯುತ್ತದೆ ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕಿರಣ, ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗದ ಪ್ರಸರಣದ ವೇಗವು ಬೆಳಕಿನ ವೇಗಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಎಂದು ತೋರಿಸಿದೆ. ಹರ್ಟ್ಜ್‌ನ ಪ್ರಾಯೋಗಿಕ ಕೆಲಸವು ಮ್ಯಾಕ್ಸ್‌ವೆಲ್‌ನ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಸಿದ್ಧಾಂತದ ಅಂಗೀಕಾರದ ಕಡೆಗೆ ಅಂತಿಮ ಹಂತವಾಗಿದೆ. ಏಳು ವರ್ಷಗಳ ನಂತರ, 1895 ರಲ್ಲಿ, ರಷ್ಯಾದ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಅಲೆಕ್ಸಾಂಡರ್ ಸ್ಟೆಪನೋವಿಚ್ ಪೊಪೊವ್ ವೈರ್ಲೆಸ್ ಸಂವಹನವನ್ನು ರಚಿಸಲು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳನ್ನು ಬಳಸಿದರು.

ವೇಗವರ್ಧಿತ ಚಲಿಸುವ ಶುಲ್ಕಗಳಿಂದ ಮಾತ್ರ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಉತ್ಸುಕವಾಗುತ್ತವೆ

ನೇರ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳಲ್ಲಿ, ಚಾರ್ಜ್‌ಗಳು ಸ್ಥಿರ ವೇಗದಲ್ಲಿ ಚಲಿಸುತ್ತವೆ ಮತ್ತು ಈ ಸಂದರ್ಭದಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳು ಬಾಹ್ಯಾಕಾಶಕ್ಕೆ ಹೊರಸೂಸುವುದಿಲ್ಲ, ವಿಕಿರಣ ಇರಬೇಕಾದರೆ, ಪರ್ಯಾಯ ಪ್ರವಾಹಗಳು, ಅಂದರೆ ಪ್ರವಾಹಗಳು ಇರುವ ಆಂಟೆನಾವನ್ನು ಬಳಸುವುದು ಅವಶ್ಯಕ. ತ್ವರಿತವಾಗಿ ತಮ್ಮ ದಿಕ್ಕನ್ನು ಬದಲಾಯಿಸಲು, ಉತ್ಸುಕರಾಗುತ್ತಾರೆ.

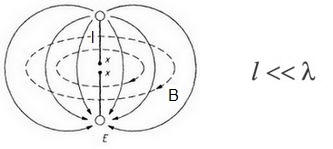
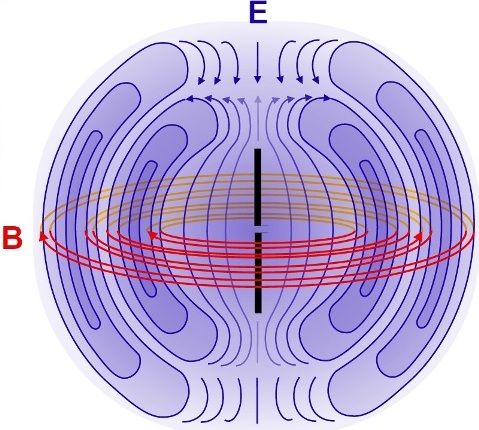
ಅದರ ಸರಳ ರೂಪದಲ್ಲಿ, ಸಣ್ಣ ಗಾತ್ರದ ವಿದ್ಯುತ್ ದ್ವಿಧ್ರುವಿಯು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳನ್ನು ಹೊರಸೂಸಲು ಸೂಕ್ತವಾಗಿದೆ, ಅಲ್ಲಿ ದ್ವಿಧ್ರುವಿ ಕ್ಷಣವು ಸಮಯದೊಂದಿಗೆ ವೇಗವಾಗಿ ಬದಲಾಗುತ್ತದೆ. ಅಂತಹ ದ್ವಿಧ್ರುವಿಯನ್ನು ಇಂದು "ಹರ್ಟ್ಜಿಯನ್ ದ್ವಿಧ್ರುವಿ" ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದರ ಗಾತ್ರವು ಅದು ಹೊರಸೂಸುವ ತರಂಗಾಂತರಕ್ಕಿಂತ ಹಲವಾರು ಪಟ್ಟು ಚಿಕ್ಕದಾಗಿದೆ.

ಹರ್ಟ್ಜಿಯನ್ ದ್ವಿಧ್ರುವಿಯಿಂದ ಹೊರಸೂಸಿದಾಗ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯ ಗರಿಷ್ಠ ಹರಿವು ದ್ವಿಧ್ರುವಿಯ ಅಕ್ಷಕ್ಕೆ ಲಂಬವಾಗಿರುವ ಸಮತಲದ ಮೇಲೆ ಬೀಳುತ್ತದೆ. ದ್ವಿಧ್ರುವಿಯ ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಯ ವಿಕಿರಣವಿಲ್ಲ. ಹರ್ಟ್ಜ್‌ನ ಅತ್ಯಂತ ಪ್ರಮುಖ ಪ್ರಯೋಗಗಳಲ್ಲಿ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ಅಸ್ತಿತ್ವವನ್ನು ಸಾಬೀತುಪಡಿಸುವ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳನ್ನು ಹೊರಸೂಸಲು ಮತ್ತು ಸ್ವೀಕರಿಸಲು ಪ್ರಾಥಮಿಕ ದ್ವಿಧ್ರುವಿಗಳನ್ನು ಬಳಸಲಾಯಿತು.