ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ಸುರುಳಿಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ

ಸ್ಥಾಯಿ ವಿದ್ಯುದಾವೇಶಗಳ ಸುತ್ತಲಿನ ಜಾಗದಲ್ಲಿ ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಕ್ಷೇತ್ರವು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ, ಚಲಿಸುವ ಚಾರ್ಜ್‌ಗಳ ಸುತ್ತಲಿನ ಜಾಗದಲ್ಲಿ (ಹಾಗೆಯೇ ಮೂಲತಃ ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಪ್ರಸ್ತಾಪಿಸಿದ ಸಮಯ-ಬದಲಾಗುವ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರಗಳ ಸುತ್ತಲೂ) ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ. ಕಾಂತೀಯ ಕ್ಷೇತ್ರ… ಇದು ಪ್ರಾಯೋಗಿಕವಾಗಿ ವೀಕ್ಷಿಸಲು ಸುಲಭವಾಗಿದೆ.

ಕಾಂತೀಯ ಕ್ಷೇತ್ರಕ್ಕೆ ಧನ್ಯವಾದಗಳು, ವಿದ್ಯುತ್ ಪ್ರವಾಹಗಳು ಪರಸ್ಪರ ಸಂವಹನ ನಡೆಸುತ್ತವೆ, ಹಾಗೆಯೇ ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳು ಮತ್ತು ಆಯಸ್ಕಾಂತಗಳೊಂದಿಗೆ ಪ್ರವಾಹಗಳು. ವಿದ್ಯುತ್ ಸಂವಹನಕ್ಕೆ ಹೋಲಿಸಿದರೆ, ಕಾಂತೀಯ ಸಂವಹನವು ಹೆಚ್ಚು ಬಲವಾಗಿರುತ್ತದೆ. ಈ ಸಂವಾದವನ್ನು ಆಂಡ್ರೆ-ಮೇರಿ ಆಂಪಿಯರ್ ಅವರು ಸರಿಯಾದ ಸಮಯದಲ್ಲಿ ಅಧ್ಯಯನ ಮಾಡಿದರು.

ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಲಕ್ಷಣವಾಗಿದೆ ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಬಿ ಮತ್ತು ಅದು ದೊಡ್ಡದಾಗಿದೆ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಬಲವಾಗಿರುತ್ತದೆ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಬಿ ಒಂದು ವೆಕ್ಟರ್ ಪ್ರಮಾಣವಾಗಿದೆ, ಅದರ ದಿಕ್ಕು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಕೆಲವು ಹಂತದಲ್ಲಿ ಇರಿಸಲಾದ ಸಾಂಪ್ರದಾಯಿಕ ಕಾಂತೀಯ ಬಾಣದ ಉತ್ತರ ಧ್ರುವದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲದ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ - ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ವೆಕ್ಟರ್ನ ದಿಕ್ಕಿನಲ್ಲಿ ಕಾಂತೀಯ ಬಾಣವನ್ನು ಓರಿಯಂಟ್ ಮಾಡುತ್ತದೆ. ಬಿ , ಅಂದರೆ, ಕಾಂತಕ್ಷೇತ್ರದ ದಿಕ್ಕಿನಲ್ಲಿ .

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ರೇಖೆಯ ಯಾವುದೇ ಹಂತದಲ್ಲಿ ವೆಕ್ಟರ್ ಬಿ ಅನ್ನು ಸ್ಪರ್ಶವಾಗಿ ನಿರ್ದೇಶಿಸಲಾಗುತ್ತದೆ. ಅಂದರೆ, ಇಂಡಕ್ಷನ್ ಬಿ ಪ್ರಸ್ತುತದ ಮೇಲೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಬಲದ ಪರಿಣಾಮವನ್ನು ನಿರೂಪಿಸುತ್ತದೆ. ಇದೇ ರೀತಿಯ ಪಾತ್ರವನ್ನು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರಕ್ಕಾಗಿ ಇ ಬಲದಿಂದ ಆಡಲಾಗುತ್ತದೆ, ಇದು ಚಾರ್ಜ್ನಲ್ಲಿ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಬಲವಾದ ಕ್ರಿಯೆಯನ್ನು ನಿರೂಪಿಸುತ್ತದೆ.

ಕಬ್ಬಿಣದ ಫೈಲಿಂಗ್‌ಗಳೊಂದಿಗಿನ ಸರಳವಾದ ಪ್ರಯೋಗವು ಕಾಂತೀಯ ವಸ್ತುವಿನ ಮೇಲೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಕ್ರಿಯೆಯ ವಿದ್ಯಮಾನವನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ಪ್ರದರ್ಶಿಸಲು ನಿಮಗೆ ಅನುಮತಿಸುತ್ತದೆ, ಏಕೆಂದರೆ ಸ್ಥಿರವಾದ ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ಫೆರೋಮ್ಯಾಗ್ನೆಟ್‌ನ ಸಣ್ಣ ತುಂಡುಗಳು (ಅಂತಹ ತುಂಡುಗಳು ಕಬ್ಬಿಣದ ಫೈಲಿಂಗ್‌ಗಳು) ಕ್ಷೇತ್ರದ ಉದ್ದಕ್ಕೂ ಕಾಂತೀಯಗೊಳಿಸಲ್ಪಡುತ್ತವೆ , ಕಾಂತೀಯ ಬಾಣಗಳು, ದಿಕ್ಸೂಚಿಯ ಸಣ್ಣ ಬಾಣಗಳಂತೆ.

ನೀವು ಲಂಬವಾದ ತಾಮ್ರದ ತಂತಿಯನ್ನು ತೆಗೆದುಕೊಂಡು ಅದನ್ನು ಅಡ್ಡಲಾಗಿ ಇರಿಸಲಾದ ಕಾಗದದ ಹಾಳೆಯಲ್ಲಿ (ಅಥವಾ ಪ್ಲೆಕ್ಸಿಗ್ಲಾಸ್ ಅಥವಾ ಪ್ಲೈವುಡ್) ರಂಧ್ರದ ಮೂಲಕ ಓಡಿಸಿದರೆ ಮತ್ತು ನಂತರ ಲೋಹದ ಫೈಲಿಂಗ್‌ಗಳನ್ನು ಹಾಳೆಯ ಮೇಲೆ ಸುರಿಯಿರಿ, ಅದನ್ನು ಸ್ವಲ್ಪ ಅಲ್ಲಾಡಿಸಿ ಮತ್ತು ನಂತರ ತಂತಿಯ ಮೂಲಕ ನೇರ ಪ್ರವಾಹವನ್ನು ಚಲಾಯಿಸಿ, ಫೈಲಿಂಗ್‌ಗಳು ತಂತಿಯ ಸುತ್ತಲಿನ ವಲಯಗಳಲ್ಲಿ, ಅದರಲ್ಲಿರುವ ಪ್ರವಾಹಕ್ಕೆ ಲಂಬವಾಗಿರುವ ಸಮತಲದಲ್ಲಿ ಸುಳಿಯ ರೂಪದಲ್ಲಿ ಹೇಗೆ ಜೋಡಿಸಲ್ಪಡುತ್ತವೆ ಎಂಬುದನ್ನು ನೋಡುವುದು ಸುಲಭ.

ಮರದ ಪುಡಿನ ಈ ವಲಯಗಳು ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ವಾಹಕದ ಕಾಂತಕ್ಷೇತ್ರದ ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ B ಯ ರೇಖೆಗಳ ಸಾಂಪ್ರದಾಯಿಕ ಪ್ರಾತಿನಿಧ್ಯವಾಗಿರುತ್ತದೆ. ಈ ಪ್ರಯೋಗದಲ್ಲಿನ ವಲಯಗಳ ಮಧ್ಯಭಾಗವು ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ತಂತಿಯ ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ ನಿಖರವಾಗಿ ಕೇಂದ್ರದಲ್ಲಿ ನೆಲೆಗೊಳ್ಳುತ್ತದೆ.

ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ತಂತಿಯಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್‌ಗಳ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸಲು ಸುಲಭವಾಗಿದೆ ಗಿಮ್ಲೆಟ್ ನಿಯಮದಿಂದ ಅಥವಾ ಬಲಗೈ ಸ್ಕ್ರೂ ನಿಯಮದ ಪ್ರಕಾರ: ತಂತಿಯಲ್ಲಿನ ಪ್ರವಾಹದ ದಿಕ್ಕಿನಲ್ಲಿ ಸ್ಕ್ರೂ ಅಕ್ಷದ ಅನುವಾದ ಚಲನೆಯೊಂದಿಗೆ, ಸ್ಕ್ರೂ ಅಥವಾ ಗಿಂಬಲ್ ಹ್ಯಾಂಡಲ್ನ ತಿರುಗುವಿಕೆಯ ದಿಕ್ಕು (ಸ್ಕ್ರೂಯಿಂಗ್ ಇನ್ ಅಥವಾ ಔಟ್) ದಿಕ್ಕನ್ನು ಸೂಚಿಸುತ್ತದೆ ಪ್ರಸ್ತುತ ಸುತ್ತಲಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ.

ಗಿಂಬಲ್ ನಿಯಮವನ್ನು ಏಕೆ ಅನ್ವಯಿಸಲಾಗಿದೆ? ಎರಡು ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಸಮೀಕರಣಗಳಲ್ಲಿ ಬಳಸಲಾದ ರೋಟರ್‌ನ ಕೆಲಸವನ್ನು (ಕ್ಷಯದಿಂದ ಕ್ಷೇತ್ರ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಸೂಚಿಸಲಾಗುತ್ತದೆ) ಔಪಚಾರಿಕವಾಗಿ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವಾಗಿ (ಆಪರೇಟರ್ ನಬ್ಲಾದೊಂದಿಗೆ) ಬರೆಯಬಹುದು ಮತ್ತು ಮುಖ್ಯವಾಗಿ ವೆಕ್ಟರ್ ಕ್ಷೇತ್ರದ ರೋಟರ್ ಅನ್ನು ಹೋಲಿಸಬಹುದು ( ಸಾದೃಶ್ಯ) ಆದರ್ಶ ದ್ರವದ ತಿರುಗುವಿಕೆಯ ಕೋನೀಯ ವೇಗಕ್ಕೆ (ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ಸ್ವತಃ ಕಲ್ಪಿಸಿಕೊಂಡಂತೆ), ಅದರ ಹರಿವಿನ ವೇಗ ಕ್ಷೇತ್ರವು ನಿರ್ದಿಷ್ಟ ವೆಕ್ಟರ್ ಕ್ಷೇತ್ರವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ, ಕೋನೀಯ ವೇಗಕ್ಕೆ ವಿವರಿಸಲಾದ ಈ ನಿಯಮ ಸೂತ್ರಗಳ ಮೂಲಕ ರೋಟರ್‌ಗೆ ಬಳಸಬಹುದು.

ಹೀಗಾಗಿ, ನೀವು ಹೆಬ್ಬೆರಳನ್ನು ವೆಕ್ಟರ್ ಕ್ಷೇತ್ರದ ಸುಳಿಯ ದಿಕ್ಕಿನಲ್ಲಿ ತಿರುಗಿಸಿದರೆ, ಅದು ಆ ಕ್ಷೇತ್ರದ ರೋಟರ್ ವೆಕ್ಟರ್ನ ದಿಕ್ಕಿನಲ್ಲಿ ಸ್ಕ್ರೂ ಆಗುತ್ತದೆ.

ನೀವು ನೋಡುವಂತೆ, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ತೆರೆದಿರುವ ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಕ್ಷೇತ್ರದ ತೀವ್ರತೆಯ ರೇಖೆಗಳಿಗಿಂತ ಭಿನ್ನವಾಗಿ, ವಿದ್ಯುತ್ ಪ್ರವಾಹವನ್ನು ಸುತ್ತುವರೆದಿರುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ರೇಖೆಗಳನ್ನು ಮುಚ್ಚಲಾಗುತ್ತದೆ. ವಿದ್ಯುತ್ ತೀವ್ರತೆಯ E ಯ ರೇಖೆಗಳು ಧನಾತ್ಮಕ ಶುಲ್ಕಗಳೊಂದಿಗೆ ಪ್ರಾರಂಭವಾದರೆ ಮತ್ತು ಋಣಾತ್ಮಕ ಶುಲ್ಕಗಳೊಂದಿಗೆ ಕೊನೆಗೊಂಡರೆ, ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ B ಯ ರೇಖೆಗಳು ಅವುಗಳನ್ನು ಉತ್ಪಾದಿಸುವ ಪ್ರವಾಹದ ಸುತ್ತಲೂ ಸರಳವಾಗಿ ಮುಚ್ಚುತ್ತವೆ.

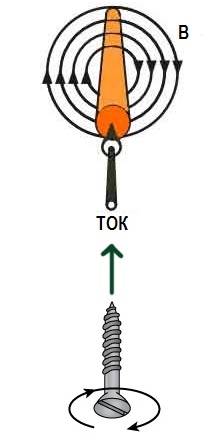
ಈಗ ಪ್ರಯೋಗವನ್ನು ಸಂಕೀರ್ಣಗೊಳಿಸೋಣ. ಪ್ರಸ್ತುತದೊಂದಿಗೆ ನೇರವಾದ ತಂತಿಯ ಬದಲಿಗೆ, ಪ್ರಸ್ತುತದೊಂದಿಗೆ ಬೆಂಡ್ ಅನ್ನು ಪರಿಗಣಿಸಿ. ರೇಖಾಚಿತ್ರದ ಸಮತಲಕ್ಕೆ ಲಂಬವಾಗಿ ಅಂತಹ ಲೂಪ್ ಅನ್ನು ಇರಿಸಲು ನಮಗೆ ಅನುಕೂಲಕರವಾಗಿದೆ ಎಂದು ಭಾವಿಸೋಣ, ಪ್ರಸ್ತುತವು ಎಡಭಾಗದಲ್ಲಿ ಮತ್ತು ನಮ್ಮಿಂದ ಬಲಕ್ಕೆ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ. ಈಗ ಆಯಸ್ಕಾಂತೀಯ ಸೂಜಿಯೊಂದಿಗೆ ದಿಕ್ಸೂಚಿಯನ್ನು ಪ್ರಸ್ತುತ ಲೂಪ್ನೊಳಗೆ ಇರಿಸಿದರೆ, ಆಯಸ್ಕಾಂತೀಯ ಸೂಜಿಯು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ರೇಖೆಗಳ ದಿಕ್ಕನ್ನು ಸೂಚಿಸುತ್ತದೆ - ಅವುಗಳನ್ನು ಲೂಪ್ನ ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ ನಿರ್ದೇಶಿಸಲಾಗುತ್ತದೆ.

ಏಕೆ? ಸುರುಳಿಯ ಸಮತಲದ ಎದುರು ಬದಿಗಳು ಕಾಂತೀಯ ಸೂಜಿಯ ಧ್ರುವಗಳಿಗೆ ಹೋಲುತ್ತವೆ.ಬಿ ರೇಖೆಗಳು ಹೊರಡುವ ಉತ್ತರ ಕಾಂತೀಯ ಧ್ರುವ, ಅಲ್ಲಿ ಅವರು ದಕ್ಷಿಣ ಧ್ರುವವನ್ನು ಪ್ರವೇಶಿಸುತ್ತಾರೆ. ನೀವು ಮೊದಲು ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ತಂತಿ ಮತ್ತು ಅದರ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಪರಿಗಣಿಸಿದರೆ, ಮತ್ತು ನಂತರ ಸರಳವಾಗಿ ತಂತಿಯನ್ನು ರಿಂಗ್ ಆಗಿ ವಿಂಡ್ ಮಾಡಿದರೆ ಇದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಸುಲಭ.

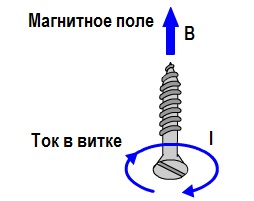
ಪ್ರವಾಹದೊಂದಿಗೆ ಲೂಪ್ನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ನ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸಲು, ಅವರು ಗಿಂಬಲ್ ನಿಯಮ ಅಥವಾ ಬಲಗೈ ಸ್ಕ್ರೂ ನಿಯಮವನ್ನು ಸಹ ಬಳಸುತ್ತಾರೆ. ಗಿಂಬಲ್‌ನ ತುದಿಯನ್ನು ಲೂಪ್‌ನ ಮಧ್ಯದಲ್ಲಿ ಇರಿಸಿ ಮತ್ತು ಅದನ್ನು ಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ ತಿರುಗಿಸಿ. ಗಿಂಬಲ್‌ನ ಅನುವಾದ ಚಲನೆಯು ಲೂಪ್‌ನ ಮಧ್ಯಭಾಗದಲ್ಲಿರುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ B ಯೊಂದಿಗೆ ದಿಕ್ಕಿನಲ್ಲಿ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ.

ನಿಸ್ಸಂಶಯವಾಗಿ, ಪ್ರವಾಹದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ದಿಕ್ಕು ತಂತಿಯಲ್ಲಿನ ಪ್ರವಾಹದ ದಿಕ್ಕಿಗೆ ಸಂಬಂಧಿಸಿದೆ, ಅದು ನೇರ ತಂತಿ ಅಥವಾ ಸುರುಳಿಯಾಗಿರಬಹುದು.

ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ಬಿ ನಿರ್ಗಮನದ ರೇಖೆಗಳು (ವೆಕ್ಟರ್ B ಯ ದಿಕ್ಕು ಹೊರಕ್ಕೆ) ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ಸುರುಳಿ ಅಥವಾ ಸುರುಳಿಯ ಬದಿಯು ಉತ್ತರ ಕಾಂತೀಯ ಧ್ರುವವಾಗಿದೆ ಮತ್ತು ರೇಖೆಗಳು ಪ್ರವೇಶಿಸುವ (ವೆಕ್ಟರ್ B ಅನ್ನು ಒಳಮುಖವಾಗಿ ನಿರ್ದೇಶಿಸಲಾಗಿದೆ) ಎಂದು ಸಾಮಾನ್ಯವಾಗಿ ಒಪ್ಪಿಕೊಳ್ಳಲಾಗಿದೆ. ದಕ್ಷಿಣ ಕಾಂತೀಯ ಧ್ರುವ.

ಪ್ರವಾಹದೊಂದಿಗೆ ಅನೇಕ ತಿರುವುಗಳು ಉದ್ದವಾದ ಸುರುಳಿಯನ್ನು ರೂಪಿಸಿದರೆ - ಸೊಲೆನಾಯ್ಡ್ (ಸುರುಳಿಯ ಉದ್ದವು ಅದರ ವ್ಯಾಸಕ್ಕಿಂತ ಹಲವು ಪಟ್ಟು), ನಂತರ ಅದರೊಳಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಏಕರೂಪವಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ B ಯ ರೇಖೆಗಳು ಪರಸ್ಪರ ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ ಮತ್ತು ಹೊಂದಿರುತ್ತವೆ ಸುರುಳಿಯ ಸಂಪೂರ್ಣ ಉದ್ದಕ್ಕೂ ಅದೇ ಸಾಂದ್ರತೆ. ಪ್ರಾಸಂಗಿಕವಾಗಿ, ಶಾಶ್ವತ ಮ್ಯಾಗ್ನೆಟ್ನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ಸುರುಳಿಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಕ್ಕೆ ಬಾಹ್ಯವಾಗಿ ಹೋಲುತ್ತದೆ.

ಪ್ರಸ್ತುತ I, ಉದ್ದ l, ತಿರುವುಗಳ ಸಂಖ್ಯೆಯೊಂದಿಗೆ ಸುರುಳಿಗಾಗಿ, ನಿರ್ವಾತದಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಸಂಖ್ಯಾತ್ಮಕವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತದೆ:

ಆದ್ದರಿಂದ, ಪ್ರಸ್ತುತದೊಂದಿಗೆ ಸುರುಳಿಯೊಳಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಏಕರೂಪವಾಗಿರುತ್ತದೆ ಮತ್ತು ದಕ್ಷಿಣ ಧ್ರುವದಿಂದ ಉತ್ತರ ಧ್ರುವಕ್ಕೆ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ (ಸುರುಳಿ ಒಳಗೆ!). ಸುರುಳಿಯೊಳಗಿನ ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯು ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ಸುರುಳಿಯ ಪ್ರತಿ ಯುನಿಟ್ ಉದ್ದದ ಆಂಪಿಯರ್-ತಿರುವುಗಳ ಸಂಖ್ಯೆಗೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ.