ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕುವುದು

ಯಂತ್ರಶಾಸ್ತ್ರದಲ್ಲಿ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಹೊಂದಿರುವ ದೇಹವು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ವೇಗವರ್ಧನೆಯನ್ನು ಪ್ರತಿರೋಧಿಸುತ್ತದೆ, ಜಡತ್ವವನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ, ಹಾಗೆಯೇ ಇಂಡಕ್ಟನ್ಸ್ ವಾಹಕದಲ್ಲಿನ ಪ್ರವಾಹವನ್ನು ಬದಲಾಯಿಸುವುದನ್ನು ತಡೆಯುತ್ತದೆ, ಸ್ವಯಂ-ಇಂಡಕ್ಷನ್ EMF ಅನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ. ಇದು ಸ್ವಯಂ-ಇಂಡಕ್ಷನ್‌ನ ಇಎಮ್‌ಎಫ್ ಆಗಿದೆ, ಇದು ಪ್ರಸ್ತುತದಲ್ಲಿನ ಇಳಿಕೆ, ಅದನ್ನು ನಿರ್ವಹಿಸಲು ಪ್ರಯತ್ನಿಸುವುದು ಮತ್ತು ಪ್ರವಾಹದ ಹೆಚ್ಚಳ, ಅದನ್ನು ಕಡಿಮೆ ಮಾಡಲು ಪ್ರಯತ್ನಿಸುವುದು ಎರಡನ್ನೂ ವಿರೋಧಿಸುತ್ತದೆ.

ಸತ್ಯವೆಂದರೆ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ಪ್ರವಾಹವನ್ನು ಬದಲಾಯಿಸುವ (ಹೆಚ್ಚಿಸುವ ಅಥವಾ ಕಡಿಮೆ ಮಾಡುವ) ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ, ಈ ಪ್ರವಾಹದಿಂದ ರಚಿಸಲಾದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಸಹ ಬದಲಾಗುತ್ತದೆ, ಇದು ಮುಖ್ಯವಾಗಿ ಈ ಸರ್ಕ್ಯೂಟ್ನಿಂದ ಸೀಮಿತವಾದ ಪ್ರದೇಶದಲ್ಲಿ ಸ್ಥಳೀಕರಿಸಲ್ಪಟ್ಟಿದೆ. ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಹೆಚ್ಚಾದಂತೆ ಅಥವಾ ಕಡಿಮೆಯಾದಂತೆ, ಅದು ಸ್ವಯಂ-ಪ್ರಚೋದನೆಯ EMF ಅನ್ನು ಪ್ರೇರೇಪಿಸುತ್ತದೆ (ಲೆನ್ಜ್ ನಿಯಮದ ಪ್ರಕಾರ - ಇದಕ್ಕೆ ಕಾರಣವಾದ ಕಾರಣಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ಅಂದರೆ, ಆರಂಭದಲ್ಲಿ ಉಲ್ಲೇಖಿಸಲಾದ ಪ್ರವಾಹದ ವಿರುದ್ಧ), ಎಲ್ಲವೂ ಒಂದೇ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ. ಇಲ್ಲಿ ಇಂಡಕ್ಟನ್ಸ್ L ಅನ್ನು ಪ್ರಸ್ತುತ I ಮತ್ತು ಒಟ್ಟು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ Φ ನಡುವಿನ ಅನುಪಾತದ ಅಂಶ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಈ ಪ್ರವಾಹವು ಇವರಿಂದ ಉತ್ಪತ್ತಿಯಾಗುತ್ತದೆ:

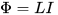
ಆದ್ದರಿಂದ, ಸರ್ಕ್ಯೂಟ್ನ ಹೆಚ್ಚಿನ ಇಂಡಕ್ಟನ್ಸ್, ಫಲಿತಾಂಶದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಕ್ಕಿಂತ ಬಲವಾಗಿರುತ್ತದೆ, ಇದು ಪ್ರವಾಹವನ್ನು ಬದಲಾಯಿಸುವುದನ್ನು ತಡೆಯುತ್ತದೆ (ಅದನ್ನು ರಚಿಸುವ ಕ್ಷೇತ್ರವಾಗಿದೆ) ಮತ್ತು ಆದ್ದರಿಂದ ಹೆಚ್ಚಿನ ಇಂಡಕ್ಟನ್ಸ್ ಮೂಲಕ ಪ್ರಸ್ತುತ ಬದಲಾಗಲು ಹೆಚ್ಚು ಸಮಯ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ, ಅದೇ ಅನ್ವಯಿಕ ವೋಲ್ಟೇಜ್ನೊಂದಿಗೆ. ಕೆಳಗಿನ ಹೇಳಿಕೆಯು ಸಹ ನಿಜವಾಗಿದೆ: ಹೆಚ್ಚಿನ ಇಂಡಕ್ಟನ್ಸ್, ಅದರ ಮೂಲಕ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಬದಲಾದಾಗ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ವೋಲ್ಟೇಜ್ ಹೆಚ್ಚಾಗುತ್ತದೆ.

ನಾವು ನಿರ್ದಿಷ್ಟ ಪ್ರದೇಶದಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ಸ್ಥಿರ ದರದಲ್ಲಿ ಬದಲಾಯಿಸುತ್ತೇವೆ ಎಂದು ಭಾವಿಸೋಣ, ನಂತರ ಈ ಪ್ರದೇಶವನ್ನು ವಿವಿಧ ಸರ್ಕ್ಯೂಟ್‌ಗಳೊಂದಿಗೆ ಮುಚ್ಚುವ ಮೂಲಕ, ಇಂಡಕ್ಟನ್ಸ್ ಹೆಚ್ಚಿರುವ ಆ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ನಾವು ಹೆಚ್ಚಿನ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ (ಟ್ರಾನ್ಸ್‌ಫಾರ್ಮರ್, ರಮ್‌ಕಾರ್ಫ್ ಕಾಯಿಲ್, ಇತ್ಯಾದಿ. ಈ ತತ್ತ್ವದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ).

ಆದರೆ ಲೂಪ್ ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕಲಾಗುತ್ತದೆ? ಪ್ರಸ್ತುತ ಮತ್ತು ಕಾಂತೀಯ ಹರಿವಿನ ನಡುವಿನ ಅನುಪಾತದ ಅಂಶವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ? ನೆನಪಿಡುವ ಮೊದಲ ವಿಷಯವೆಂದರೆ ಹೆನ್ರಿ (H) ನಲ್ಲಿ ಇಂಡಕ್ಟನ್ಸ್ ಬದಲಾಗುತ್ತದೆ. 1 ಹೆನ್ರಿ ಇಂಡಕ್ಟನ್ಸ್ ಹೊಂದಿರುವ ಸರ್ಕ್ಯೂಟ್‌ನ ಟರ್ಮಿನಲ್‌ಗಳಲ್ಲಿ, ಅದರಲ್ಲಿರುವ ಪ್ರವಾಹವು ಸೆಕೆಂಡಿಗೆ ಒಂದು ಆಂಪಿಯರ್‌ನಿಂದ ಬದಲಾದರೆ, 1 ವೋಲ್ಟ್ ವೋಲ್ಟೇಜ್ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ.

ಇಂಡಕ್ಟನ್ಸ್‌ನ ಪ್ರಮಾಣವು ಎರಡು ನಿಯತಾಂಕಗಳನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ: ಸರ್ಕ್ಯೂಟ್‌ನ ಜ್ಯಾಮಿತೀಯ ಆಯಾಮಗಳ ಮೇಲೆ (ಉದ್ದ, ಅಗಲ, ತಿರುವುಗಳ ಸಂಖ್ಯೆ, ಇತ್ಯಾದಿ) ಮತ್ತು ಮಾಧ್ಯಮದ ಕಾಂತೀಯ ಗುಣಲಕ್ಷಣಗಳ ಮೇಲೆ (ಉದಾಹರಣೆಗೆ, ಒಳಗೆ ಫೆರೈಟ್ ಕೋರ್ ಇದ್ದರೆ ಕಾಯಿಲ್, ಅದರ ಇಂಡಕ್ಟನ್ಸ್ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ, ಒಳಗೆ ಯಾವುದೇ ಕೋರ್ ಇಲ್ಲದಿದ್ದರೆ).

ಉತ್ಪತ್ತಿಯಾಗುವ ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ಸುರುಳಿಯು ಯಾವ ಆಕಾರದಲ್ಲಿದೆ ಮತ್ತು ಅದರೊಳಗಿನ ಮಾಧ್ಯಮವು ಯಾವ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ ಎಂಬುದನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು ಅವಶ್ಯಕ (ಮಾಧ್ಯಮದ ಸಾಪೇಕ್ಷ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು ನಿರ್ವಾತ ಮತ್ತು ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯ ನಡುವಿನ ಅನುಪಾತದ ಅಂಶವಾಗಿದೆ. ನಿರ್ದಿಷ್ಟ ಮಾಧ್ಯಮದ ಪ್ರವೇಶಸಾಧ್ಯತೆ.ಸಹಜವಾಗಿ, ಇದು ವಿಭಿನ್ನ ವಸ್ತುಗಳಿಗೆ ವಿಭಿನ್ನವಾಗಿದೆ) ...

ಸುರುಳಿಗಳ ಸಾಮಾನ್ಯ ರೂಪಗಳ (ಸಿಲಿಂಡರಾಕಾರದ ಸೊಲೆನಾಯ್ಡ್, ಟೊರಾಯ್ಡ್ ಮತ್ತು ಉದ್ದನೆಯ ತಂತಿ) ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸೂತ್ರಗಳನ್ನು ನೋಡೋಣ.

ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸೂತ್ರ ಇಲ್ಲಿದೆ ಸೊಲೆನಾಯ್ಡ್ - ಸುರುಳಿಗಳು, ಅದರ ಉದ್ದವು ವ್ಯಾಸಕ್ಕಿಂತ ಹೆಚ್ಚು:

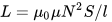
ನೀವು ನೋಡುವಂತೆ, ತಿರುವುಗಳ ಸಂಖ್ಯೆ ಎನ್, ಅಂಕುಡೊಂಕಾದ ಎಲ್ ಉದ್ದ ಮತ್ತು ಕಾಯಿಲ್ ಎಸ್ನ ಅಡ್ಡ-ವಿಭಾಗದ ಪ್ರದೇಶವನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದರಿಂದ, ಕೋರ್ ಇಲ್ಲದೆ ಅಥವಾ ಕೋರ್ನೊಂದಿಗೆ ಸುರುಳಿಯ ಅಂದಾಜು ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ, ಆದರೆ ಕಾಂತೀಯ ನಿರ್ವಾತದ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು ಸ್ಥಿರ ಮೌಲ್ಯವಾಗಿದೆ:

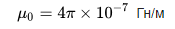
ಟೊರೊಯ್ಡಲ್ ಕಾಯಿಲ್‌ನ ಇಂಡಕ್ಟನ್ಸ್, ಇಲ್ಲಿ h ಎಂಬುದು ಟೊರಾಯ್ಡ್‌ನ ಎತ್ತರ, r ಎಂಬುದು ಟೊರಾಯ್ಡ್‌ನ ಒಳಗಿನ ವ್ಯಾಸ, R ಎಂಬುದು ಟೊರಾಯ್ಡ್‌ನ ಹೊರಗಿನ ವ್ಯಾಸ:

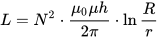
ತೆಳುವಾದ ತಂತಿಯ ಇಂಡಕ್ಟನ್ಸ್ (ಅಡ್ಡ-ವಿಭಾಗದ ತ್ರಿಜ್ಯವು ಉದ್ದಕ್ಕಿಂತ ಚಿಕ್ಕದಾಗಿದೆ), ಇಲ್ಲಿ l ಎಂಬುದು ತಂತಿಯ ಉದ್ದ ಮತ್ತು r ಅದರ ಅಡ್ಡ-ವಿಭಾಗದ ತ್ರಿಜ್ಯವಾಗಿದೆ. I ಮತ್ತು e ಸೂಚ್ಯಂಕಗಳೊಂದಿಗೆ Mu. ಆಂತರಿಕ (ಆಂತರಿಕ, ಕಂಡಕ್ಟರ್ ವಸ್ತುಗಳು) ಮತ್ತು ಬಾಹ್ಯ (ಬಾಹ್ಯ, ವಾಹಕದ ಹೊರಗಿನ ವಸ್ತುಗಳು) ಪರಿಸರದ ಸಾಪೇಕ್ಷ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಗಳು:

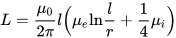
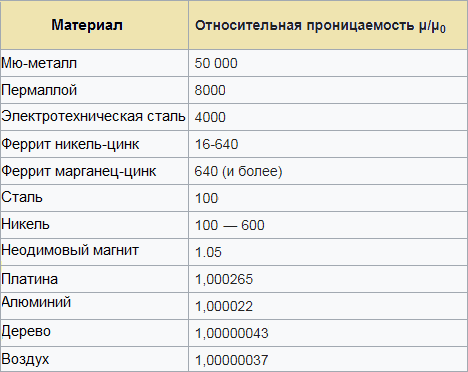
ನಿರ್ದಿಷ್ಟ ಕಾಂತೀಯ ವಸ್ತುವನ್ನು ಕೋರ್ ಆಗಿ ಬಳಸಿಕೊಂಡು ಸರ್ಕ್ಯೂಟ್ (ವೈರ್, ಕಾಯಿಲ್) ನಿಂದ ನೀವು ಯಾವ ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ನಿರೀಕ್ಷಿಸಬಹುದು ಎಂಬುದನ್ನು ಅಂದಾಜು ಮಾಡಲು ಸಾಪೇಕ್ಷ ಅನುಮತಿಗಳ ಕೋಷ್ಟಕವು ನಿಮಗೆ ಸಹಾಯ ಮಾಡುತ್ತದೆ: