ಇಂಡಕ್ಟನ್ಸ್ ಎಂದರೇನು
ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಆದರ್ಶೀಕರಿಸಿದ ಅಂಶ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಇದರಲ್ಲಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ಸಂಗ್ರಹಿಸಲಾಗುತ್ತದೆ. ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ಸಂಗ್ರಹಣೆ ಅಥವಾ ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಇತರ ರೀತಿಯ ಶಕ್ತಿಯಾಗಿ ಪರಿವರ್ತಿಸುವುದು ಅದರಲ್ಲಿ ಸಂಭವಿಸುವುದಿಲ್ಲ.
ಆದರ್ಶೀಕರಿಸಿದ ಅಂಶಕ್ಕೆ ಹತ್ತಿರದ ವಿಷಯ - ಇಂಡಕ್ಟನ್ಸ್ - ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ನಿಜವಾದ ಅಂಶವಾಗಿದೆ - ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್.
ಇಂಡಕ್ಟನ್ಸ್ಗಿಂತ ಭಿನ್ನವಾಗಿ, ಇಂಡಕ್ಟನ್ಸ್ ಕಾಯಿಲ್ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ಸಂಗ್ರಹಿಸುತ್ತದೆ ಮತ್ತು ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಇತರ ರೀತಿಯ ಶಕ್ತಿಯಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ, ನಿರ್ದಿಷ್ಟವಾಗಿ ಶಾಖ.
ಪರಿಮಾಣಾತ್ಮಕವಾಗಿ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ಸಂಗ್ರಹಿಸಲು ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ನೈಜ ಮತ್ತು ಆದರ್ಶೀಕರಿಸಿದ ಅಂಶಗಳ ಸಾಮರ್ಥ್ಯವು ಇಂಡಕ್ಟನ್ಸ್ ಎಂಬ ನಿಯತಾಂಕದಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟಿದೆ.
ಹೀಗಾಗಿ, "ಇಂಡಕ್ಟನ್ಸ್" ಎಂಬ ಪದವನ್ನು ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಆದರ್ಶೀಕರಿಸಿದ ಅಂಶದ ಹೆಸರಾಗಿ, ಈ ಅಂಶದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಪರಿಮಾಣಾತ್ಮಕವಾಗಿ ನಿರೂಪಿಸುವ ನಿಯತಾಂಕದ ಹೆಸರಾಗಿ ಮತ್ತು ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ನ ಮುಖ್ಯ ನಿಯತಾಂಕದ ಹೆಸರಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ.
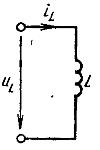
ಅಕ್ಕಿ. 1. ಇಂಡಕ್ಟನ್ಸ್ನ ಸಾಂಪ್ರದಾಯಿಕ ಚಿತ್ರಾತ್ಮಕ ಸಂಕೇತ
ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ನಲ್ಲಿ ವೋಲ್ಟೇಜ್ ಮತ್ತು ಪ್ರವಾಹದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ನಿಯಮ, ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ ಅನ್ನು ಭೇದಿಸುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಬದಲಾದಾಗ, ಅದರಲ್ಲಿ ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಇ ಅನ್ನು ಪ್ರೇರೇಪಿಸುತ್ತದೆ, ಇದು ಸುರುಳಿಯ ಫ್ಲಕ್ಸ್ ಲಿಂಕ್ನ ಬದಲಾವಣೆಯ ದರಕ್ಕೆ ಅನುಗುಣವಾಗಿ ψ ಮತ್ತು ಪ್ರವಾಹವು ಉಂಟಾಗುವ ರೀತಿಯಲ್ಲಿ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ ಇದು ಕಾಂತೀಯ ಹರಿವಿನ ಬದಲಾವಣೆಯನ್ನು ತಡೆಯುತ್ತದೆ:
e = — dψ / dt
ಸುರುಳಿಯ ಹರಿವಿನ ಸಂಪರ್ಕವು ಅದರ ಪ್ರತ್ಯೇಕ ತಿರುವುಗಳನ್ನು ಭೇದಿಸುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ಗಳ ಬೀಜಗಣಿತ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
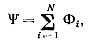
ಇಲ್ಲಿ N ಎಂಬುದು ಸುರುಳಿಯ ತಿರುವುಗಳ ಸಂಖ್ಯೆ.
ಸುರುಳಿಯ ಪ್ರತಿಯೊಂದು ತಿರುವುಗಳನ್ನು ಭೇದಿಸುವ ಕಾಂತೀಯ ಹರಿವು ಎಫ್, ಸಾಮಾನ್ಯ ಸಂದರ್ಭದಲ್ಲಿ, ಎರಡು ಘಟಕಗಳನ್ನು ಒಳಗೊಂಡಿರಬಹುದು: ಸ್ವಯಂ-ಇಂಡಕ್ಷನ್ Fsi ಮತ್ತು ಬಾಹ್ಯ ಕ್ಷೇತ್ರಗಳ ಕಾಂತೀಯ ಹರಿವು Fvp: F - Fsi + Fvp.
ಮೊದಲ ಅಂಶವೆಂದರೆ ಸುರುಳಿಯ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹದಿಂದ ಉಂಟಾಗುವ ಕಾಂತೀಯ ಹರಿವು, ಎರಡನೆಯದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳಿಂದ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ, ಅದರ ಅಸ್ತಿತ್ವವು ಸುರುಳಿಯಲ್ಲಿನ ಪ್ರವಾಹಕ್ಕೆ ಸಂಬಂಧಿಸಿಲ್ಲ - ಭೂಮಿಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ, ಇತರ ಸುರುಳಿಗಳ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳು ಮತ್ತು ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳು… ಆಯಸ್ಕಾಂತೀಯ ಹರಿವಿನ ಎರಡನೇ ಅಂಶವು ಮತ್ತೊಂದು ಸುರುಳಿಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಿಂದ ಉಂಟಾದರೆ, ಅದನ್ನು ಪರಸ್ಪರ ಪ್ರೇರಣೆಯ ಕಾಂತೀಯ ಹರಿವು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಕಾಯಿಲ್ ಫ್ಲಕ್ಸ್ ψ, ಹಾಗೆಯೇ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ Φ ಅನ್ನು ಎರಡು ಘಟಕಗಳ ಮೊತ್ತವಾಗಿ ಪ್ರತಿನಿಧಿಸಬಹುದು: ಸ್ವಯಂ-ಇಂಡಕ್ಷನ್ ಫ್ಲಕ್ಸ್ ಲಿಂಕೇಜ್ ψsi ಮತ್ತು ಬಾಹ್ಯ ಕ್ಷೇತ್ರ ಫ್ಲಕ್ಸ್ ಲಿಂಕೇಜ್ ψvp
ψ= ψsi + ψvp
e = esi + dvp,
ಇಲ್ಲಿ eu ಸ್ವಯಂ ಪ್ರೇರಣೆಯ EMF ಆಗಿದೆ, evp ಬಾಹ್ಯ ಕ್ಷೇತ್ರಗಳ EMF ಆಗಿದೆ.
ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ಗೆ ಹೊರಗಿನ ಕ್ಷೇತ್ರಗಳ ಕಾಂತೀಯ ಹರಿವುಗಳು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿದ್ದರೆ ಮತ್ತು ಸ್ವಯಂ ಪ್ರೇರಿತ ಫ್ಲಕ್ಸ್ ಮಾತ್ರ ಸುರುಳಿಯನ್ನು ಭೇದಿಸುತ್ತದೆ, ಆಗ ಮಾತ್ರ ಸ್ವಯಂ ಪ್ರೇರಣೆಯ EMF.
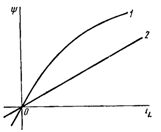
ಇಂಡಕ್ಟನ್ಸ್ ಫ್ಲಕ್ಸ್ ಸಂಬಂಧವು ಸುರುಳಿಯ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಈ ಅವಲಂಬನೆಯನ್ನು ವೆಬರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ - ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ನ ಆಂಪಿಯರ್ ಗುಣಲಕ್ಷಣವು ಸಾಮಾನ್ಯವಾಗಿ ರೇಖಾತ್ಮಕವಲ್ಲದ ಪಾತ್ರವನ್ನು ಹೊಂದಿರುತ್ತದೆ (ಚಿತ್ರ 2, ಕರ್ವ್ 1).
ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂದರ್ಭದಲ್ಲಿ, ಉದಾಹರಣೆಗೆ, ಕಾಂತೀಯ ಕೋರ್ ಇಲ್ಲದ ಸುರುಳಿಗಾಗಿ, ಈ ಅವಲಂಬನೆಯು ರೇಖೀಯವಾಗಿರಬಹುದು (ಚಿತ್ರ 2, ಕರ್ವ್ 2).
ಅಕ್ಕಿ. 2. ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ನ ವೆಬರ್-ಆಂಪಿಯರ್ನ ಗುಣಲಕ್ಷಣಗಳು: 1 - ರೇಖಾತ್ಮಕವಲ್ಲದ, 2 - ರೇಖೀಯ.
SI ಘಟಕಗಳಲ್ಲಿ, ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಹೆನ್ರಿಸ್ (H) ನಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ.
ಸರ್ಕ್ಯೂಟ್ಗಳನ್ನು ವಿಶ್ಲೇಷಿಸುವಾಗ, ಸುರುಳಿಯಲ್ಲಿ ಪ್ರೇರಿತವಾದ ಇಎಮ್ಎಫ್ನ ಮೌಲ್ಯವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವುದಿಲ್ಲ, ಆದರೆ ಅದರ ಟರ್ಮಿನಲ್ಗಳಲ್ಲಿನ ವೋಲ್ಟೇಜ್, ಅದರ ಸಕಾರಾತ್ಮಕ ದಿಕ್ಕನ್ನು ಪ್ರಸ್ತುತದ ಧನಾತ್ಮಕ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುವಂತೆ ಆಯ್ಕೆ ಮಾಡಲಾಗುತ್ತದೆ:
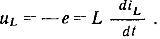
ಎಲೆಕ್ಟ್ರಿಕಲ್ ಸರ್ಕ್ಯೂಟ್ನ ಆದರ್ಶೀಕರಿಸಿದ ಅಂಶ - ಇಂಡಕ್ಟನ್ಸ್ - ಇಂಡಕ್ಟಿವ್ ಕಾಯಿಲ್ನ ಸರಳೀಕೃತ ಮಾದರಿಯಾಗಿ ಕಾಣಬಹುದು, ಇದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ಸಂಗ್ರಹಿಸುವ ಸುರುಳಿಯ ಸಾಮರ್ಥ್ಯವನ್ನು ಪ್ರತಿಬಿಂಬಿಸುತ್ತದೆ.
ರೇಖೀಯ ಇಂಡಕ್ಟನ್ಸ್ಗಾಗಿ, ಅದರ ಟರ್ಮಿನಲ್ಗಳಲ್ಲಿನ ವೋಲ್ಟೇಜ್ ಪ್ರಸ್ತುತದ ಬದಲಾವಣೆಯ ದರಕ್ಕೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. ನೇರ ಪ್ರವಾಹವು ಇಂಡಕ್ಟನ್ಸ್ ಮೂಲಕ ಹರಿಯುವಾಗ, ಅದರ ಟರ್ಮಿನಲ್ಗಳಲ್ಲಿನ ವೋಲ್ಟೇಜ್ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ನೇರ ಪ್ರವಾಹಕ್ಕೆ ಇಂಡಕ್ಟನ್ಸ್ನ ಪ್ರತಿರೋಧವು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ.