ನಷ್ಟಗಳು ಮತ್ತು ವೋಲ್ಟೇಜ್ ಹನಿಗಳು - ವ್ಯತ್ಯಾಸಗಳು ಯಾವುವು

ಸಾಮಾನ್ಯ ಮಾನವ ಜೀವನದಲ್ಲಿ, "ನಷ್ಟ" ಮತ್ತು "ಪತನ" ಪದಗಳನ್ನು ಕೆಲವು ಸಾಧನೆಗಳಲ್ಲಿನ ಇಳಿಕೆಯ ಅಂಶವನ್ನು ಸೂಚಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ, ಆದರೆ ಅವು ವಿಭಿನ್ನ ಮೌಲ್ಯವನ್ನು ಅರ್ಥೈಸುತ್ತವೆ.

ಈ ಸಂದರ್ಭದಲ್ಲಿ, "ನಷ್ಟಗಳು" ಎಂದರೆ ಒಂದು ಭಾಗದ ನಷ್ಟ, ಹಾನಿ, ಹಿಂದೆ ಸಾಧಿಸಿದ ಮಟ್ಟದ ಗಾತ್ರವನ್ನು ಕಡಿಮೆ ಮಾಡುವುದು. ನಷ್ಟಗಳು ಅನಪೇಕ್ಷಿತ, ಆದರೆ ನೀವು ಅವುಗಳನ್ನು ಸಹಿಸಿಕೊಳ್ಳಬಹುದು.

"ಪತನ" ಎಂಬ ಪದವನ್ನು ಹಕ್ಕುಗಳ ಸಂಪೂರ್ಣ ಅಭಾವಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಹೆಚ್ಚು ಗಂಭೀರ ಹಾನಿ ಎಂದು ಅರ್ಥೈಸಲಾಗುತ್ತದೆ. ಹೀಗಾಗಿ, ಕಾಲಾನಂತರದಲ್ಲಿ ಸಾಂದರ್ಭಿಕವಾಗಿ ಸಂಭವಿಸುವ ನಷ್ಟಗಳು (ಹೇಳಲು, ಪೋರ್ಟ್ಫೋಲಿಯೊ) ಕುಸಿತಕ್ಕೆ ಕಾರಣವಾಗಬಹುದು (ಉದಾಹರಣೆಗೆ, ವಸ್ತು ಜೀವನದ ಮಟ್ಟ).

ಈ ನಿಟ್ಟಿನಲ್ಲಿ, ವಿದ್ಯುತ್ ಜಾಲದ ವೋಲ್ಟೇಜ್ಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ನಾವು ಈ ಪ್ರಶ್ನೆಯನ್ನು ಪರಿಗಣಿಸುತ್ತೇವೆ.

ನಷ್ಟಗಳು ಮತ್ತು ವೋಲ್ಟೇಜ್ ಹನಿಗಳು ಹೇಗೆ ರೂಪುಗೊಳ್ಳುತ್ತವೆ

ಒಂದು ಸಬ್‌ಸ್ಟೇಷನ್‌ನಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಓವರ್‌ಹೆಡ್ ಲೈನ್‌ಗಳ ಮೂಲಕ ವಿದ್ಯುತ್ ಅನ್ನು ದೂರದವರೆಗೆ ಸಾಗಿಸಲಾಗುತ್ತದೆ.

ಓವರ್ಹೆಡ್ ಲೈನ್ಗಳನ್ನು ಅನುಮತಿಸುವ ಶಕ್ತಿಯನ್ನು ರವಾನಿಸಲು ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ ಮತ್ತು ನಿರ್ದಿಷ್ಟ ವಸ್ತು ಮತ್ತು ವಿಭಾಗದ ಲೋಹದ ತಂತಿಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟಿದೆ. ಅವರು R ನ ಪ್ರತಿರೋಧ ಮೌಲ್ಯ ಮತ್ತು X ನ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಲೋಡ್ನೊಂದಿಗೆ ಪ್ರತಿರೋಧಕ ಲೋಡ್ ಅನ್ನು ರಚಿಸುತ್ತಾರೆ.

ಸ್ವೀಕರಿಸುವ ಬದಿಯಲ್ಲಿ ಅದು ನಿಂತಿದೆ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ವಿದ್ಯುತ್ ಪರಿವರ್ತನೆ.ಇದರ ಸುರುಳಿಗಳು ಸಕ್ರಿಯ ಮತ್ತು ಉಚ್ಚರಿಸಲಾದ ಅನುಗಮನದ ಪ್ರತಿರೋಧ XL ಅನ್ನು ಹೊಂದಿವೆ. ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ದ್ವಿತೀಯಕ ಭಾಗವು ವೋಲ್ಟೇಜ್ ಅನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ಗ್ರಾಹಕರಿಗೆ ಮತ್ತಷ್ಟು ರವಾನಿಸುತ್ತದೆ, ಅವರ ಲೋಡ್ ಅನ್ನು Z ನ ಮೌಲ್ಯದಿಂದ ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಪ್ರಕೃತಿಯಲ್ಲಿ ಸಕ್ರಿಯ, ಕೆಪ್ಯಾಸಿಟಿವ್ ಮತ್ತು ಇಂಡಕ್ಟಿವ್ ಆಗಿದೆ. ಇದು ನೆಟ್ವರ್ಕ್ನ ವಿದ್ಯುತ್ ನಿಯತಾಂಕಗಳನ್ನು ಸಹ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ.

ವಿದ್ಯುತ್ ಪ್ರಸರಣ ಸಬ್‌ಸ್ಟೇಷನ್‌ಗೆ ಸಮೀಪವಿರುವ ಓವರ್‌ಹೆಡ್ ಲೈನ್‌ನ ಬೆಂಬಲದ ತಂತಿಗಳಿಗೆ ಅನ್ವಯಿಸಲಾದ ವೋಲ್ಟೇಜ್ ಪ್ರತಿ ಹಂತದಲ್ಲಿ ಸರ್ಕ್ಯೂಟ್‌ನ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಮತ್ತು ಸಕ್ರಿಯ ಪ್ರತಿರೋಧವನ್ನು ಮೀರಿಸುತ್ತದೆ ಮತ್ತು ಅದರಲ್ಲಿ ಪ್ರವಾಹವನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ, ಅದರ ವೆಕ್ಟರ್ ವೆಕ್ಟರ್‌ನಿಂದ ವಿಚಲನಗೊಳ್ಳುತ್ತದೆ. φ ಕೋನದಿಂದ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಅನ್ವಯಿಸಲಾಗಿದೆ.

ವೋಲ್ಟೇಜ್ಗಳ ವಿತರಣೆಯ ಸ್ವರೂಪ ಮತ್ತು ಸಮ್ಮಿತೀಯ ಲೋಡ್ ಮೋಡ್ಗಾಗಿ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ಪ್ರವಾಹಗಳ ಹರಿವು ಫೋಟೋದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ.

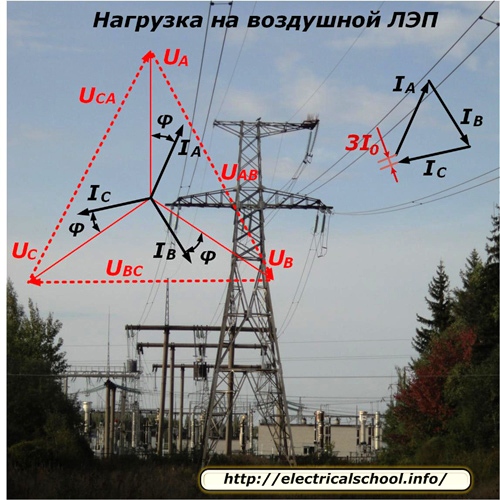
ಸಾಲಿನ ಪ್ರತಿಯೊಂದು ಹಂತವು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಸಂಪರ್ಕ ಕಡಿತಗೊಂಡ ಅಥವಾ ಕೆಲಸಕ್ಕೆ ಸಂಪರ್ಕ ಹೊಂದಿದ ವಿಭಿನ್ನ ಸಂಖ್ಯೆಯ ಗ್ರಾಹಕರಿಗೆ ಆಹಾರವನ್ನು ನೀಡುವುದರಿಂದ, ಹಂತದ ಹೊರೆಯನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಸಮತೋಲನಗೊಳಿಸುವುದು ತಾಂತ್ರಿಕವಾಗಿ ತುಂಬಾ ಕಷ್ಟಕರವಾಗಿದೆ. ಅದರಲ್ಲಿ ಯಾವಾಗಲೂ ಅಸಮತೋಲನವಿದೆ, ಇದು ಹಂತದ ಪ್ರವಾಹಗಳ ವೆಕ್ಟರ್ ಸೇರ್ಪಡೆಯಿಂದ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ ಮತ್ತು 3I0 ಎಂದು ಬರೆಯಲಾಗುತ್ತದೆ. ಹೆಚ್ಚಿನ ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ, ಇದನ್ನು ಸರಳವಾಗಿ ನಿರ್ಲಕ್ಷಿಸಲಾಗುತ್ತದೆ.

ಟ್ರಾನ್ಸ್ಮಿಟಿಂಗ್ ಸಬ್‌ಸ್ಟೇಷನ್‌ನಿಂದ ಸೇವಿಸುವ ಶಕ್ತಿಯು ರೇಖೆಯ ಪ್ರತಿರೋಧವನ್ನು ಮೀರಿಸಲು ಭಾಗಶಃ ಖರ್ಚುಮಾಡುತ್ತದೆ ಮತ್ತು ಸ್ವಲ್ಪ ಬದಲಾವಣೆಯೊಂದಿಗೆ ಸ್ವೀಕರಿಸುವ ಭಾಗವನ್ನು ತಲುಪುತ್ತದೆ. ಈ ಭಾಗವನ್ನು ನಷ್ಟ ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ ಮೂಲಕ ನಿರೂಪಿಸಲಾಗಿದೆ, ಇದರ ವೆಕ್ಟರ್ ವೈಶಾಲ್ಯದಲ್ಲಿ ಸ್ವಲ್ಪ ಕಡಿಮೆಯಾಗುತ್ತದೆ ಮತ್ತು ಪ್ರತಿ ಹಂತದಲ್ಲಿ ಕೋನದಿಂದ ಬದಲಾಯಿಸಲ್ಪಡುತ್ತದೆ.

ನಷ್ಟಗಳು ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ ಅನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕಲಾಗುತ್ತದೆ

ವಿದ್ಯುತ್ ಪ್ರಸರಣದ ಸಮಯದಲ್ಲಿ ನಡೆಯುವ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು, ಮುಖ್ಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸಲು ವೆಕ್ಟರ್ ರೂಪವು ಅನುಕೂಲಕರವಾಗಿದೆ. ವಿವಿಧ ಗಣಿತದ ಲೆಕ್ಕಾಚಾರದ ವಿಧಾನಗಳು ಸಹ ಈ ವಿಧಾನವನ್ನು ಆಧರಿಸಿವೆ.

ಲೆಕ್ಕಾಚಾರಗಳನ್ನು ಸರಳಗೊಳಿಸಲು ಮೂರು-ಹಂತದ ವ್ಯವಸ್ಥೆ ಇದನ್ನು ಮೂರು ಏಕ-ಹಂತದ ಸಮಾನ ಸರ್ಕ್ಯೂಟ್‌ಗಳಿಂದ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ. ಈ ವಿಧಾನವು ಸಮ್ಮಿತೀಯ ಹೊರೆಯೊಂದಿಗೆ ಉತ್ತಮವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ ಮತ್ತು ಅದು ಮುರಿದಾಗ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ವಿಶ್ಲೇಷಿಸಲು ನಿಮಗೆ ಅನುಮತಿಸುತ್ತದೆ.

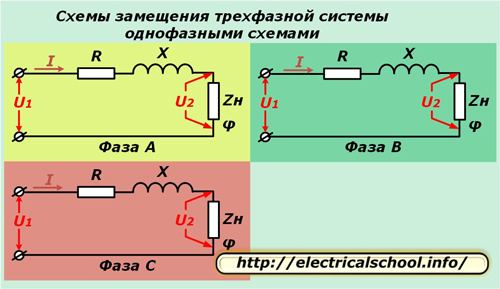
ಮೇಲಿನ ರೇಖಾಚಿತ್ರಗಳಲ್ಲಿ, ರೇಖೆಯ ಪ್ರತಿ ಕಂಡಕ್ಟರ್‌ನ ಸಕ್ರಿಯ R ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ X ಅನ್ನು ಕೋನ φ ನಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟ ಸಂಕೀರ್ಣ ಲೋಡ್ ಪ್ರತಿರೋಧ Zn ನೊಂದಿಗೆ ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಲಾಗಿದೆ.

ಇದರ ಜೊತೆಗೆ, ಒಂದು ಹಂತದಲ್ಲಿ ವೋಲ್ಟೇಜ್ ನಷ್ಟ ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ನ ಲೆಕ್ಕಾಚಾರವನ್ನು ನಡೆಸಲಾಗುತ್ತದೆ. ಇದನ್ನು ಮಾಡಲು, ನೀವು ಡೇಟಾವನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಬೇಕು. ಈ ಉದ್ದೇಶಕ್ಕಾಗಿ, ಶಕ್ತಿಯನ್ನು ಪಡೆಯುವ ಸಬ್‌ಸ್ಟೇಷನ್ ಅನ್ನು ಆಯ್ಕೆಮಾಡಲಾಗುತ್ತದೆ, ಅಲ್ಲಿ ಅನುಮತಿಸುವ ಲೋಡ್ ಅನ್ನು ಈಗಾಗಲೇ ನಿರ್ಧರಿಸಬೇಕು.

ಯಾವುದೇ ಉನ್ನತ-ವೋಲ್ಟೇಜ್ ಸಿಸ್ಟಮ್ನ ವೋಲ್ಟೇಜ್ ಮೌಲ್ಯವನ್ನು ಈಗಾಗಲೇ ಉಲ್ಲೇಖ ಪುಸ್ತಕಗಳಲ್ಲಿ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಮತ್ತು ತಂತಿಗಳ ಪ್ರತಿರೋಧಗಳನ್ನು ಅವುಗಳ ಉದ್ದ, ಅಡ್ಡ-ವಿಭಾಗ, ವಸ್ತು ಮತ್ತು ನೆಟ್ವರ್ಕ್ನ ಸಂರಚನೆಯಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ಗರಿಷ್ಠ ಪ್ರವಾಹವನ್ನು ತಂತಿಗಳ ಗುಣಲಕ್ಷಣಗಳಿಂದ ಹೊಂದಿಸಲಾಗಿದೆ ಮತ್ತು ಸೀಮಿತಗೊಳಿಸಲಾಗಿದೆ.

ಆದ್ದರಿಂದ, ಲೆಕ್ಕಾಚಾರಗಳನ್ನು ಪ್ರಾರಂಭಿಸಲು, ನಾವು ಹೊಂದಿದ್ದೇವೆ: U2, R, X, Z, I, φ.

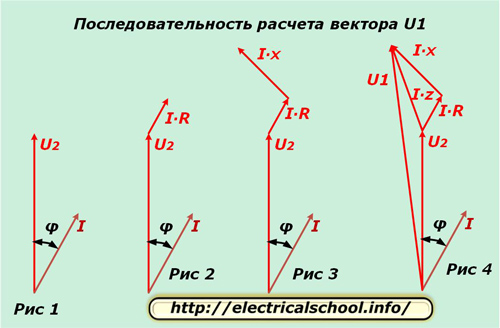
ನಾವು ಒಂದು ಹಂತವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ, ಉದಾಹರಣೆಗೆ, "ಎ" ಮತ್ತು ಸಂಕೀರ್ಣ ಸಮತಲದಲ್ಲಿ ವಾಹಕಗಳು U2 ಮತ್ತು I ಅನ್ನು ಪ್ರತ್ಯೇಕಿಸಿ, ಚಿತ್ರ 1 ರಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ φ ಕೋನದಿಂದ ಸ್ಥಳಾಂತರಿಸಲಾಗುತ್ತದೆ. ವಾಹಕದ ಸಕ್ರಿಯ ಪ್ರತಿರೋಧದಲ್ಲಿನ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು ದಿಕ್ಕಿನಲ್ಲಿ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ. ಪ್ರಸ್ತುತದೊಂದಿಗೆ ಮತ್ತು ಪರಿಮಾಣದಲ್ಲಿ I ∙ R. ನಾವು U2 (Fig. 2) ನ ಅಂತ್ಯದಿಂದ ಈ ವೆಕ್ಟರ್ ಅನ್ನು ಮುಂದೂಡುತ್ತೇವೆ ಎಂಬ ಅಭಿವ್ಯಕ್ತಿಯಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ವಾಹಕದ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕತೆಯ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು φ1 ಕೋನದಿಂದ ಪ್ರಸ್ತುತದ ದಿಕ್ಕಿನಿಂದ ಭಿನ್ನವಾಗಿದೆ ಮತ್ತು ಉತ್ಪನ್ನ I ∙ X ನಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ನಾವು ಅದನ್ನು ವೆಕ್ಟರ್ I ∙ R (Fig. 3) ನಿಂದ ಮುಂದೂಡುತ್ತೇವೆ.

ಜ್ಞಾಪನೆಗಳು: ಸಂಕೀರ್ಣ ಸಮತಲದಲ್ಲಿ ವಾಹಕಗಳ ತಿರುಗುವಿಕೆಯ ಧನಾತ್ಮಕ ನಿರ್ದೇಶನಕ್ಕಾಗಿ, ಅಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ ಚಲನೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಇಂಡಕ್ಟಿವ್ ಲೋಡ್ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹವು ಕೋನದಿಂದ ಅನ್ವಯಿಕ ವೋಲ್ಟೇಜ್ ಅನ್ನು ವಿಳಂಬಗೊಳಿಸುತ್ತದೆ.

ಚಿತ್ರ 4 ಒಟ್ಟು ತಂತಿ ಪ್ರತಿರೋಧ I ∙ Z ಮತ್ತು ಸರ್ಕ್ಯೂಟ್ U1 ನ ಇನ್ಪುಟ್ನಲ್ಲಿನ ವೋಲ್ಟೇಜ್ನಲ್ಲಿ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸ ವೆಕ್ಟರ್ಗಳ ಪ್ಲಾಟಿಂಗ್ ಅನ್ನು ತೋರಿಸುತ್ತದೆ.

ಈಗ ನೀವು ಇನ್‌ಪುಟ್ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಸಮಾನ ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಮತ್ತು ಲೋಡ್‌ನಾದ್ಯಂತ ಹೋಲಿಸಬಹುದು. ಇದನ್ನು ಮಾಡಲು, ಪರಿಣಾಮವಾಗಿ ರೇಖಾಚಿತ್ರವನ್ನು ಅಡ್ಡಲಾಗಿ (Fig. 5) ಹಾಕಿ ಮತ್ತು ವೆಕ್ಟರ್ U2 (Fig. 6) ನ ದಿಕ್ಕಿನೊಂದಿಗೆ ಛೇದಿಸುವವರೆಗೆ ಮಾಡ್ಯೂಲ್ U1 ನ ತ್ರಿಜ್ಯದೊಂದಿಗೆ ಪ್ರಾರಂಭದಿಂದ ಒಂದು ಆರ್ಕ್ ಅನ್ನು ಎಳೆಯಿರಿ.

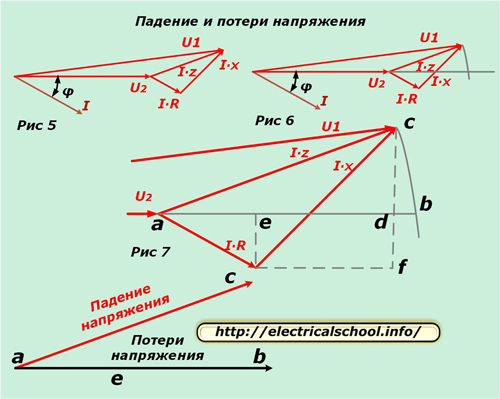
ಚಿತ್ರ 7 ಹೆಚ್ಚಿನ ಸ್ಪಷ್ಟತೆಗಾಗಿ ತ್ರಿಕೋನದ ಹಿಗ್ಗುವಿಕೆ ಮತ್ತು ಸಹಾಯಕ ರೇಖೆಗಳ ರೇಖಾಚಿತ್ರವನ್ನು ತೋರಿಸುತ್ತದೆ, ಇದು ಅಕ್ಷರಗಳೊಂದಿಗೆ ಛೇದನದ ವಿಶಿಷ್ಟ ಬಿಂದುಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ.

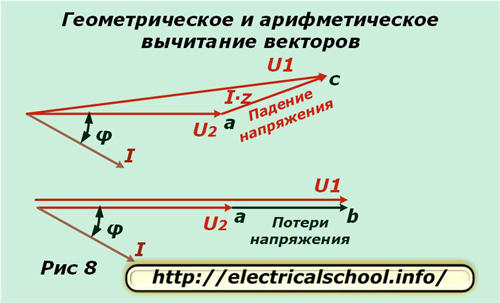
ಚಿತ್ರದ ಕೆಳಭಾಗದಲ್ಲಿ ಪರಿಣಾಮವಾಗಿ ವೆಕ್ಟರ್ ಎಸಿ ಅನ್ನು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಎಬಿ ಅನ್ನು ನಷ್ಟ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅವು ಗಾತ್ರ ಮತ್ತು ದಿಕ್ಕಿನಲ್ಲಿ ಭಿನ್ನವಾಗಿರುತ್ತವೆ. ನಾವು ಮೂಲ ಮಾಪಕಕ್ಕೆ ಹಿಂತಿರುಗಿದರೆ, ವೆಕ್ಟರ್‌ಗಳ ಜ್ಯಾಮಿತೀಯ ವ್ಯವಕಲನದ ಪರಿಣಾಮವಾಗಿ ac ಅನ್ನು ಪಡೆಯಲಾಗಿದೆ ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ (U1 ನಿಂದ U2), ಮತ್ತು ab ಅಂಕಗಣಿತವಾಗಿದೆ. ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ (ಚಿತ್ರ 8).

ವೋಲ್ಟೇಜ್ ನಷ್ಟಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸೂತ್ರಗಳ ವ್ಯುತ್ಪನ್ನ

ಈಗ ಚಿತ್ರ 7 ಕ್ಕೆ ಹಿಂತಿರುಗಿ ಬಿಡಿ ಮತ್ತು ಬಿಡಿ ವಿಭಾಗವು ತುಂಬಾ ಚಿಕ್ಕದಾಗಿದೆ ಎಂದು ಗಮನಿಸೋಣ. ಈ ಕಾರಣಕ್ಕಾಗಿ, ಇದನ್ನು ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ ನಿರ್ಲಕ್ಷಿಸಲಾಗಿದೆ ಮತ್ತು ವಿಭಾಗದ ಉದ್ದದ ಜಾಹೀರಾತಿನಿಂದ ವೋಲ್ಟೇಜ್ ನಷ್ಟವನ್ನು ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ಇದು ae ಮತ್ತು ed ಎಂಬ ಎರಡು ಸಾಲಿನ ವಿಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿದೆ.

ae = I ∙ R ∙ cosφ ಮತ್ತು ed = I ∙ x ∙ sinφ, ನಂತರ ಒಂದು ಹಂತದ ವೋಲ್ಟೇಜ್ ನಷ್ಟವನ್ನು ಸೂತ್ರದ ಮೂಲಕ ಲೆಕ್ಕ ಹಾಕಬಹುದು:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

ಎಲ್ಲಾ ಹಂತಗಳಲ್ಲಿ ಲೋಡ್ ಸಮ್ಮಿತೀಯವಾಗಿದೆ ಎಂದು ನಾವು ಭಾವಿಸಿದರೆ (ಷರತ್ತುಬದ್ಧವಾಗಿ 3I0 ಅನ್ನು ನಿರ್ಲಕ್ಷಿಸುವುದು), ಸಾಲಿನಲ್ಲಿ ವೋಲ್ಟೇಜ್ ನಷ್ಟವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ನಾವು ಗಣಿತದ ವಿಧಾನಗಳನ್ನು ಬಳಸಬಹುದು.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

ಈ ಸೂತ್ರದ ಬಲಭಾಗವನ್ನು ನೆಟ್ವರ್ಕ್ ವೋಲ್ಟೇಜ್ Un ನಿಂದ ಗುಣಿಸಿದರೆ ಮತ್ತು ಭಾಗಿಸಿದರೆ, ನಾವು ವಿದ್ಯುತ್ ಸರಬರಾಜಿನ ಮೂಲಕ ವೋಲ್ಟೇಜ್ ನಷ್ಟಗಳ pCalculation ಅನ್ನು ನಿರ್ವಹಿಸಲು ನಮಗೆ ಅನುಮತಿಸುವ ಸೂತ್ರವನ್ನು ಪಡೆಯುತ್ತೇವೆ.

∆Ul = (P ∙ r + Q ∙ x) / Un

ಸಕ್ರಿಯ P ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ Q ಶಕ್ತಿಯ ಮೌಲ್ಯಗಳನ್ನು ಲೈನ್ ಮೀಟರ್ ವಾಚನಗಳಿಂದ ತೆಗೆದುಕೊಳ್ಳಬಹುದು.

ಹೀಗಾಗಿ, ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ವೋಲ್ಟೇಜ್ ನಷ್ಟವು ಅವಲಂಬಿಸಿರುತ್ತದೆ:

• ಸರ್ಕ್ಯೂಟ್ನ ಸಕ್ರಿಯ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯೆ;

• ಅನ್ವಯಿಕ ಶಕ್ತಿಯ ಘಟಕಗಳು;

• ಅನ್ವಯಿಕ ವೋಲ್ಟೇಜ್ನ ಪ್ರಮಾಣ.

ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ನ ಟ್ರಾನ್ಸ್ವರ್ಸ್ ಘಟಕವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸೂತ್ರಗಳ ವ್ಯುತ್ಪನ್ನ

ಚಿತ್ರ 7ಕ್ಕೆ ಹಿಂತಿರುಗಿ ನೋಡೋಣ. ವೆಕ್ಟರ್ ಎಸಿಯ ಮೌಲ್ಯವನ್ನು ಬಲ ತ್ರಿಕೋನ ಎಸಿಡಿಯ ಹೈಪೊಟೆನ್ಯೂಸ್‌ನಿಂದ ಪ್ರತಿನಿಧಿಸಬಹುದು. ನಾವು ಈಗಾಗಲೇ ಜಾಹೀರಾತು ಅಡಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡಿದ್ದೇವೆ. ಅಡ್ಡ ಕಾಂಪೊನೆಂಟ್ CD ಅನ್ನು ನಾವು ನಿರ್ಧರಿಸೋಣ.

ಚಿತ್ರವು cd = cf-df ಎಂದು ತೋರಿಸುತ್ತದೆ.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

ಪಡೆದ ಮಾದರಿಗಳನ್ನು ಬಳಸಿಕೊಂಡು, ನಾವು ಸಣ್ಣ ಗಣಿತದ ರೂಪಾಂತರಗಳನ್ನು ನಿರ್ವಹಿಸುತ್ತೇವೆ ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ನ ಟ್ರಾನ್ಸ್ವರ್ಸ್ ಘಟಕವನ್ನು ಪಡೆಯುತ್ತೇವೆ.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

ವಿದ್ಯುತ್ ಲೈನ್ನ ಆರಂಭದಲ್ಲಿ ವೋಲ್ಟೇಜ್ U1 ಅನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸೂತ್ರದ ನಿರ್ಣಯ

U2 ರೇಖೆಯ ಕೊನೆಯಲ್ಲಿ ವೋಲ್ಟೇಜ್ನ ಮೌಲ್ಯವನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು, ನಷ್ಟ ∆Ul ಮತ್ತು ಡ್ರಾಪ್ δU ನ ಅಡ್ಡ ಘಟಕ, ನಾವು ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯದಿಂದ ವೆಕ್ಟರ್ U1 ನ ಮೌಲ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಬಹುದು. ವಿಸ್ತರಿತ ರೂಪದಲ್ಲಿ, ಇದು ಕೆಳಗಿನ ರೂಪವನ್ನು ಹೊಂದಿದೆ.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

ಪ್ರಾಯೋಗಿಕ ಬಳಕೆ

ನೆಟ್ವರ್ಕ್ನ ಸಂರಚನೆ ಮತ್ತು ಅದರ ಘಟಕ ಅಂಶಗಳ ಅತ್ಯುತ್ತಮ ಆಯ್ಕೆಗಾಗಿ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ ಯೋಜನೆಯನ್ನು ರಚಿಸುವ ಹಂತದಲ್ಲಿ ವೋಲ್ಟೇಜ್ ನಷ್ಟಗಳ ಲೆಕ್ಕಾಚಾರವನ್ನು ಎಂಜಿನಿಯರ್ಗಳು ನಡೆಸುತ್ತಾರೆ.

ವಿದ್ಯುತ್ ಅನುಸ್ಥಾಪನೆಯ ಕಾರ್ಯಾಚರಣೆಯ ಸಮಯದಲ್ಲಿ, ಅಗತ್ಯವಿದ್ದರೆ, ರೇಖೆಗಳ ತುದಿಯಲ್ಲಿರುವ ವೋಲ್ಟೇಜ್ ವೆಕ್ಟರ್ಗಳ ಏಕಕಾಲಿಕ ಅಳತೆಗಳನ್ನು ನಿಯತಕಾಲಿಕವಾಗಿ ಕೈಗೊಳ್ಳಬಹುದು ಮತ್ತು ಸರಳ ಲೆಕ್ಕಾಚಾರಗಳ ವಿಧಾನದಿಂದ ಪಡೆದ ಫಲಿತಾಂಶಗಳನ್ನು ಹೋಲಿಸಬಹುದು.ಈ ವಿಧಾನವು ಹೆಚ್ಚಿದ ಸಾಧನಗಳಿಗೆ ಸೂಕ್ತವಾಗಿದೆ. ಹೆಚ್ಚಿನ ಕೆಲಸದ ನಿಖರತೆಯ ಅಗತ್ಯತೆಯಿಂದಾಗಿ ಅವಶ್ಯಕತೆಗಳು.

ದ್ವಿತೀಯ ಸರ್ಕ್ಯೂಟ್ಗಳಲ್ಲಿ ವೋಲ್ಟೇಜ್ ನಷ್ಟಗಳು

ವೋಲ್ಟೇಜ್ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ಗಳನ್ನು ಅಳತೆ ಮಾಡುವ ದ್ವಿತೀಯಕ ಸರ್ಕ್ಯೂಟ್ಗಳು ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ, ಇದು ಕೆಲವೊಮ್ಮೆ ಹಲವಾರು ನೂರು ಮೀಟರ್ ಉದ್ದವನ್ನು ತಲುಪುತ್ತದೆ ಮತ್ತು ಹೆಚ್ಚಿದ ಅಡ್ಡ-ವಿಭಾಗದೊಂದಿಗೆ ವಿಶೇಷ ವಿದ್ಯುತ್ ಕೇಬಲ್ನಿಂದ ಹರಡುತ್ತದೆ.

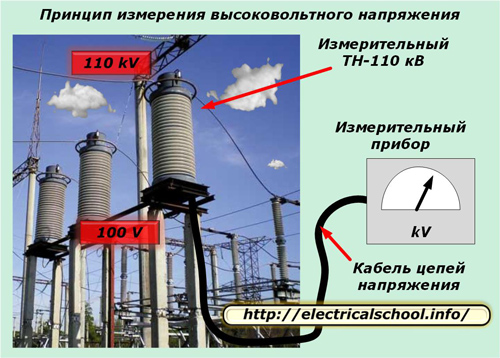
ಅಂತಹ ಕೇಬಲ್ನ ವಿದ್ಯುತ್ ಗುಣಲಕ್ಷಣಗಳು ವೋಲ್ಟೇಜ್ ಪ್ರಸರಣದ ಗುಣಮಟ್ಟಕ್ಕೆ ಹೆಚ್ಚಿದ ಅವಶ್ಯಕತೆಗಳಿಗೆ ಒಳಪಟ್ಟಿರುತ್ತವೆ.

ವಿದ್ಯುತ್ ಉಪಕರಣಗಳ ಆಧುನಿಕ ರಕ್ಷಣೆಗೆ ಹೆಚ್ಚಿನ ಮಾಪನಶಾಸ್ತ್ರದ ಸೂಚಕಗಳು ಮತ್ತು 0.5 ಅಥವಾ 0.2 ರ ನಿಖರತೆಯ ವರ್ಗದೊಂದಿಗೆ ಮಾಪನ ವ್ಯವಸ್ಥೆಗಳ ಕಾರ್ಯಾಚರಣೆಯ ಅಗತ್ಯವಿರುತ್ತದೆ. ಆದ್ದರಿಂದ, ಅವರಿಗೆ ಅನ್ವಯಿಸಲಾದ ವೋಲ್ಟೇಜ್ನ ನಷ್ಟವನ್ನು ಮೇಲ್ವಿಚಾರಣೆ ಮಾಡಬೇಕು ಮತ್ತು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಇಲ್ಲದಿದ್ದರೆ, ಉಪಕರಣದ ಕಾರ್ಯಾಚರಣೆಯಲ್ಲಿ ಅವರು ಪರಿಚಯಿಸಿದ ದೋಷವು ಎಲ್ಲಾ ಕಾರ್ಯಾಚರಣೆಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಗಮನಾರ್ಹವಾಗಿ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ.

ದೀರ್ಘ ಕೇಬಲ್ ಲೈನ್ಗಳಲ್ಲಿ ವೋಲ್ಟೇಜ್ ನಷ್ಟಗಳು

ಉದ್ದನೆಯ ಕೇಬಲ್ನ ವಿನ್ಯಾಸದ ವೈಶಿಷ್ಟ್ಯವೆಂದರೆ ಕೋರ್ಗಳನ್ನು ನಡೆಸುವ ಸಾಕಷ್ಟು ನಿಕಟ ವ್ಯವಸ್ಥೆ ಮತ್ತು ಅವುಗಳ ನಡುವೆ ತೆಳುವಾದ ಪದರದ ನಿರೋಧನದ ಕಾರಣದಿಂದಾಗಿ ಇದು ಕೆಪ್ಯಾಸಿಟಿವ್ ಪ್ರತಿರೋಧವನ್ನು ಹೊಂದಿದೆ. ಇದು ಕೇಬಲ್ ಮೂಲಕ ಹಾದುಹೋಗುವ ಪ್ರಸ್ತುತ ವೆಕ್ಟರ್ ಅನ್ನು ಮತ್ತಷ್ಟು ತಿರುಗಿಸುತ್ತದೆ ಮತ್ತು ಅದರ ಪ್ರಮಾಣವನ್ನು ಬದಲಾಯಿಸುತ್ತದೆ.

I ∙ z ನ ಮೌಲ್ಯವನ್ನು ಬದಲಾಯಿಸಲು ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ ಕೆಪ್ಯಾಸಿಟಿವ್ ಪ್ರತಿರೋಧದ ಮೇಲೆ ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ನ ಪರಿಣಾಮವನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಇಲ್ಲದಿದ್ದರೆ, ಮೇಲೆ ವಿವರಿಸಿದ ತಂತ್ರಜ್ಞಾನವು ಬದಲಾಗುವುದಿಲ್ಲ.

ಲೇಖನವು ಓವರ್ಹೆಡ್ ಪವರ್ ಲೈನ್ಗಳು ಮತ್ತು ಕೇಬಲ್ಗಳ ಮೇಲೆ ನಷ್ಟಗಳು ಮತ್ತು ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ಗಳ ಉದಾಹರಣೆಗಳನ್ನು ಒದಗಿಸುತ್ತದೆ. ಆದಾಗ್ಯೂ, ಎಲೆಕ್ಟ್ರಿಕ್ ಮೋಟರ್‌ಗಳು, ಟ್ರಾನ್ಸ್‌ಫಾರ್ಮರ್‌ಗಳು, ಇಂಡಕ್ಟರ್‌ಗಳು, ಕೆಪಾಸಿಟರ್ ಬ್ಯಾಂಕ್‌ಗಳು ಮತ್ತು ಇತರ ಸಾಧನಗಳನ್ನು ಒಳಗೊಂಡಂತೆ ವಿದ್ಯುತ್‌ನ ಎಲ್ಲಾ ಗ್ರಾಹಕರಲ್ಲಿ ಅವು ಕಂಡುಬರುತ್ತವೆ.

ಪ್ರತಿಯೊಂದು ವಿಧದ ವಿದ್ಯುತ್ ಉಪಕರಣಗಳಿಗೆ ವೋಲ್ಟೇಜ್ ನಷ್ಟಗಳ ಪ್ರಮಾಣವು ಕಾರ್ಯಾಚರಣಾ ಪರಿಸ್ಥಿತಿಗಳ ವಿಷಯದಲ್ಲಿ ಕಾನೂನುಬದ್ಧವಾಗಿ ನಿಯಂತ್ರಿಸಲ್ಪಡುತ್ತದೆ ಮತ್ತು ಎಲ್ಲಾ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ಗಳಲ್ಲಿ ಅವುಗಳ ನಿರ್ಣಯದ ತತ್ವವು ಒಂದೇ ಆಗಿರುತ್ತದೆ.