ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಎಂದರೇನು

ಈ ಲೇಖನದಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಎಂದರೇನು, ಅದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರಕ್ಕೆ ಹೇಗೆ ಸಂಬಂಧಿಸಿದೆ, ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಪ್ರಸ್ತುತದೊಂದಿಗೆ ಏನು ಮಾಡಬೇಕು ಮತ್ತು ಅದು ಪ್ರವಾಹದ ಮೇಲೆ ಹೇಗೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ನಾವು ಪ್ರಯತ್ನಿಸುತ್ತೇವೆ. ಇಂಡಕ್ಷನ್ ರೇಖೆಗಳ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸುವ ಮೂಲ ನಿಯಮಗಳನ್ನು ನಾವು ನೆನಪಿಸಿಕೊಳ್ಳೋಣ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟೋಸ್ಟಾಟಿಕ್ಸ್ನ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ಸಹಾಯ ಮಾಡುವ ಕೆಲವು ಸೂತ್ರಗಳನ್ನು ಸಹ ನಾವು ಗಮನಿಸುತ್ತೇವೆ.

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಆಯ್ದ ಬಿಂದುವಿನಲ್ಲಿ ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ವಿಶಿಷ್ಟ ಶಕ್ತಿಯು ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ B. ಈ ವೆಕ್ಟರ್ ಪ್ರಮಾಣವು ಕಾಂತಕ್ಷೇತ್ರವು ಅದರಲ್ಲಿ ಚಲಿಸುವ ಚಾರ್ಜ್ಡ್ ಕಣದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ. ಕಣದ ಚಾರ್ಜ್ q ಆಗಿದ್ದರೆ, ಅದರ ವೇಗವು v ಆಗಿದ್ದರೆ ಮತ್ತು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಬಿಂದುವಿನಲ್ಲಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ B ಆಗಿದ್ದರೆ, ಕಾಂತಕ್ಷೇತ್ರದ ಬದಿಯಿಂದ ಆ ಹಂತದಲ್ಲಿ ಒಂದು ಬಲವು ಕಣದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ:

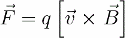
ಹೀಗಾಗಿ, B ಎಂಬುದು ವೆಕ್ಟರ್ ಆಗಿದ್ದು, ಅದರ ಪ್ರಮಾಣ ಮತ್ತು ದಿಕ್ಕು ಕಾಂತಕ್ಷೇತ್ರದ ಬದಿಯಲ್ಲಿ ಚಲಿಸುವ ಚಾರ್ಜ್‌ನಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಲೊರೆಂಟ್ಜ್ ಬಲವು ಇದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

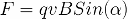
ಇಲ್ಲಿ, ಆಲ್ಫಾ ವೇಗ ವೆಕ್ಟರ್ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ ನಡುವಿನ ಕೋನವಾಗಿದೆ. ಲೊರೆಂಟ್ಜ್ ಫೋರ್ಸ್ ವೆಕ್ಟರ್ ಎಫ್ ವೇಗ ವೆಕ್ಟರ್ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್‌ಗೆ ಲಂಬವಾಗಿರುತ್ತದೆ.ಏಕರೂಪದ ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ಧನಾತ್ಮಕ ಆವೇಶದ ಕಣದ ಚಲನೆಯ ಸಂದರ್ಭದಲ್ಲಿ ಅದರ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಎಡಗೈ ನಿಯಮ:

"ಆಯಸ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವೆಕ್ಟರ್ ಅಂಗೈಗೆ ಪ್ರವೇಶಿಸುವಂತೆ ಎಡಗೈಯನ್ನು ಇರಿಸಿದರೆ ಮತ್ತು ನಾಲ್ಕು ಚಾಚಿದ ಬೆರಳುಗಳನ್ನು ಧನಾತ್ಮಕ ಆವೇಶದ ಕಣದ ಚಲನೆಯ ದಿಕ್ಕಿನಲ್ಲಿ ನಿರ್ದೇಶಿಸಿದರೆ, ಹೆಬ್ಬೆರಳು, 90 ಡಿಗ್ರಿಗಳಲ್ಲಿ ಬಾಗಿ, ದಿಕ್ಕನ್ನು ತೋರಿಸುತ್ತದೆ. ಲೊರೆಂಟ್ಜ್ ಫೋರ್ಸ್.»

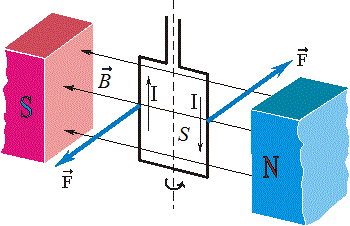
ವಾಹಕದಲ್ಲಿನ ಪ್ರವಾಹವು ಚಾರ್ಜ್ಡ್ ಕಣಗಳ ಚಲನೆಯಾಗಿರುವುದರಿಂದ, ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯು ಚೌಕಟ್ಟಿನಲ್ಲಿನ ಏಕರೂಪದ ಕಾಂತಕ್ಷೇತ್ರದೊಂದಿಗೆ ಚೌಕಟ್ಟಿನ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಗರಿಷ್ಠ ಯಾಂತ್ರಿಕ ಕ್ಷಣದ ಅನುಪಾತವಾಗಿ ಚೌಕಟ್ಟಿನಲ್ಲಿನ ಪ್ರವಾಹದ ಉತ್ಪನ್ನಕ್ಕೆ ವಿಸ್ತೀರ್ಣದಿಂದ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು. ಚೌಕಟ್ಟು:

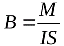
ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಒಂದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಮೂಲಭೂತ ಲಕ್ಷಣವಾಗಿದೆ, ಇದು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಬಲವನ್ನು ಹೋಲುತ್ತದೆ... SI ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಅನ್ನು ಟೆಸ್ಲಾ (T), CGS ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಗಾಸ್ (G) ನಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ. 1 ಟೆಸ್ಲಾ = 10,000 ಗಾಸ್. 1 ಟಿ ಅಂತಹ ಏಕರೂಪದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಪ್ರಚೋದನೆಯಾಗಿದ್ದು, ಇದರಲ್ಲಿ 1 N • m ಗೆ ಸಮಾನವಾದ ಶಕ್ತಿಗಳ ಗರಿಷ್ಠ ತಿರುಗುವ ಯಾಂತ್ರಿಕ ಕ್ಷಣವು 1 m2 ಪ್ರದೇಶದ ಚೌಕಟ್ಟಿನ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಅದರ ಮೂಲಕ 1 A ಪ್ರವಾಹವು ಹರಿಯುತ್ತದೆ.

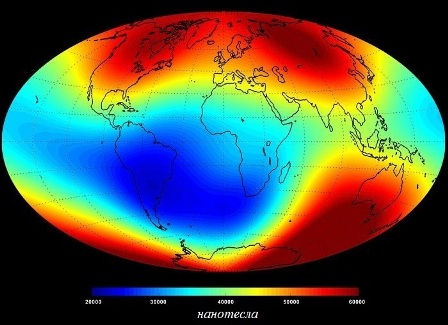
ಮೂಲಕ, 50 ° ಅಕ್ಷಾಂಶದಲ್ಲಿ ಭೂಮಿಯ ಕಾಂತಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ ಸರಾಸರಿ 0.00005 T, ಮತ್ತು ಸಮಭಾಜಕದಲ್ಲಿ - 0.000031 T. ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ ಯಾವಾಗಲೂ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗೆ ಸ್ಪರ್ಶವಾಗಿ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತದೆ.

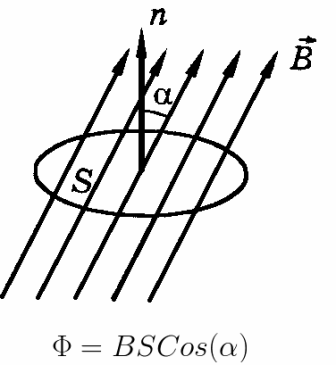
ಏಕರೂಪದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಲಾದ ಲೂಪ್ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ Ф, - ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ನ ಫ್ಲಕ್ಸ್ನಿಂದ ಭೇದಿಸಲ್ಪಡುತ್ತದೆ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ನ ಪ್ರಮಾಣವು ಬಾಹ್ಯರೇಖೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ನ ದಿಕ್ಕು, ಅದರ ಪ್ರಮಾಣ ಮತ್ತು ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ರೇಖೆಗಳಿಂದ ಚುಚ್ಚಿದ ಬಾಹ್ಯರೇಖೆಯ ಪ್ರದೇಶವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.ವೆಕ್ಟರ್ ಬಿ ಲೂಪ್ನ ಪ್ರದೇಶಕ್ಕೆ ಲಂಬವಾಗಿದ್ದರೆ, ಲೂಪ್ ಅನ್ನು ಭೇದಿಸುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಗರಿಷ್ಠವಾಗಿರುತ್ತದೆ.

ಇಂಡಕ್ಷನ್ ಎಂಬ ಪದವು ಲ್ಯಾಟಿನ್ "ಇಂಡಕ್ಷನ್" ನಿಂದ ಬಂದಿದೆ, ಇದರರ್ಥ "ಮಾರ್ಗದರ್ಶನ" (ಉದಾಹರಣೆಗೆ ಆಲೋಚನೆಯನ್ನು ಸೂಚಿಸಲು - ಅಂದರೆ, ಆಲೋಚನೆಯನ್ನು ಉಂಟುಮಾಡಲು). ಸಮಾನಾರ್ಥಕ: ಮಾರ್ಗದರ್ಶನ, ಹಿನ್ನೆಲೆ, ಶಿಕ್ಷಣ. ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವಿದ್ಯಮಾನದೊಂದಿಗೆ ಗೊಂದಲಕ್ಕೀಡಾಗಬಾರದು.

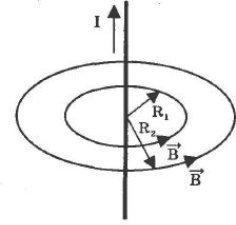
ಅದರ ಸುತ್ತಲೂ ಲೈವ್ ವೈರ್ ಇದೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ… ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು 1820 ರಲ್ಲಿ ಡ್ಯಾನಿಶ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಹ್ಯಾನ್ಸ್ ಕ್ರಿಶ್ಚಿಯನ್ ಓರ್ಸ್ಟೆಡ್ ಕಂಡುಹಿಡಿದನು. ನೇರ ತಂತಿಯ ಉದ್ದಕ್ಕೂ ಹರಿಯುವ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ B ಯ ಕಾಂತಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ನ ಬಲದ ರೇಖೆಗಳ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸಲು, ಬಲಗೈ ಸ್ಕ್ರೂ ಅಥವಾ ಗಿಂಬಲ್ ನಿಯಮವನ್ನು ಬಳಸಿ:

"ಗಿಂಬಲ್ ಹ್ಯಾಂಡಲ್ನ ತಿರುಗುವಿಕೆಯ ದಿಕ್ಕು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಬಿ ರೇಖೆಗಳ ದಿಕ್ಕನ್ನು ಸೂಚಿಸುತ್ತದೆ, ಮತ್ತು ಗಿಂಬಲ್ನ ಪ್ರಗತಿಶೀಲ ಚಲನೆಯು ವಾಹಕದಲ್ಲಿನ ಪ್ರವಾಹದ ದಿಕ್ಕಿಗೆ ಅನುರೂಪವಾಗಿದೆ."

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ವಿದ್ಯುತ್ I ನೊಂದಿಗೆ ಕಂಡಕ್ಟರ್‌ನಿಂದ R ದೂರದಲ್ಲಿರುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ B ಯ ಮೌಲ್ಯವನ್ನು ಸೂತ್ರದಿಂದ ಕಂಡುಹಿಡಿಯಬಹುದು:

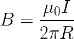
ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕ ಎಲ್ಲಿದೆ:

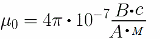
ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಕ್ಷೇತ್ರ E ಯ ತೀವ್ರತೆಯ ರೇಖೆಗಳು, ಧನಾತ್ಮಕ ಶುಲ್ಕಗಳಿಂದ ಪ್ರಾರಂಭಿಸಿ, ಋಣಾತ್ಮಕ ಪದಗಳಿಗಿಂತ ಕೊನೆಗೊಂಡರೆ, ನಂತರ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ B ಯ ರೇಖೆಗಳು ಯಾವಾಗಲೂ ಮುಚ್ಚಲ್ಪಡುತ್ತವೆ. ವಿದ್ಯುದಾವೇಶಗಳಂತೆ, ವಿದ್ಯುದಾವೇಶಗಳಂತಹ ಧ್ರುವಗಳನ್ನು ಸೃಷ್ಟಿಸುವ ಕಾಂತೀಯ ಶುಲ್ಕಗಳು ಪ್ರಕೃತಿಯಲ್ಲಿ ಕಂಡುಬಂದಿಲ್ಲ.

ಈಗ ಕೆಲವು ಪದಗಳು ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳ ಬಗ್ಗೆ… 19 ನೇ ಶತಮಾನದ ಆರಂಭದಲ್ಲಿ, ಫ್ರೆಂಚ್ ಸಂಶೋಧಕ ಮತ್ತು ನೈಸರ್ಗಿಕ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಆಂಡ್ರೆ-ಮೇರಿ ಆಂಪಿಯರ್ ಆಣ್ವಿಕ ಪ್ರವಾಹಗಳ ಬಗ್ಗೆ ಒಂದು ಊಹೆಯನ್ನು ಪ್ರಸ್ತಾಪಿಸಿದರು. ಆಂಪಿಯರ್ ಪ್ರಕಾರ, ಪರಮಾಣು ನ್ಯೂಕ್ಲಿಯಸ್‌ಗಳ ಸುತ್ತ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳ ಚಲನೆಯು ಪ್ರಾಥಮಿಕ ಪ್ರವಾಹಗಳನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ, ಅದು ಅವುಗಳ ಸುತ್ತಲೂ ಪ್ರಾಥಮಿಕ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ.ಮತ್ತು ಫೆರೋಮ್ಯಾಗ್ನೆಟ್‌ನ ತುಂಡನ್ನು ಬಾಹ್ಯ ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಿದರೆ, ಈ ಸೂಕ್ಷ್ಮ ಆಯಸ್ಕಾಂತಗಳು ಬಾಹ್ಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ತಮ್ಮನ್ನು ಓರಿಯಂಟ್ ಮಾಡುತ್ತದೆ ಮತ್ತು ಫೆರೋಮ್ಯಾಗ್ನೆಟ್ ತುಂಡು ಮ್ಯಾಗ್ನೆಟ್ ಆಗುತ್ತದೆ.

ನಿಯೋಡೈಮಿಯಮ್-ಐರನ್-ಬೋರಾನ್ ಮಿಶ್ರಲೋಹದಂತಹ ಹೆಚ್ಚಿನ ಉಳಿದಿರುವ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಮೌಲ್ಯವನ್ನು ಹೊಂದಿರುವ ವಸ್ತುಗಳು ಇಂದು ಶಕ್ತಿಯುತ ಶಾಶ್ವತ ಆಯಸ್ಕಾಂತಗಳನ್ನು ಪಡೆಯಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ. ನಿಯೋಡೈಮಿಯಮ್ ಆಯಸ್ಕಾಂತಗಳು 10 ವರ್ಷಗಳಲ್ಲಿ ತಮ್ಮ ಕಾಂತೀಯೀಕರಣದ 1-2% ಕ್ಕಿಂತ ಹೆಚ್ಚು ಕಳೆದುಕೊಳ್ಳುವುದಿಲ್ಲ. ಆದರೆ + 70 ° C ಅಥವಾ ಹೆಚ್ಚಿನ ತಾಪಮಾನಕ್ಕೆ ಬಿಸಿ ಮಾಡುವ ಮೂಲಕ ಅವುಗಳನ್ನು ಸುಲಭವಾಗಿ ಡಿಮ್ಯಾಗ್ನೆಟೈಸ್ ಮಾಡಬಹುದು.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಎಂದರೇನು ಮತ್ತು ಅದು ಎಲ್ಲಿಂದ ಬರುತ್ತದೆ ಎಂಬ ಸಾಮಾನ್ಯ ಕಲ್ಪನೆಯನ್ನು ಪಡೆಯಲು ಈ ಲೇಖನವು ನಿಮಗೆ ಸಹಾಯ ಮಾಡಿದೆ ಎಂದು ನಾವು ಭಾವಿಸುತ್ತೇವೆ.