ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಾಗಿ ಓಮ್ನ ನಿಯಮ

ಯಾವುದೇ ಕಾಂತೀಯ ಹರಿವುಗಳಿಲ್ಲದಿದ್ದರೆ, ಆಧುನಿಕ ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್ ಅಸ್ತಿತ್ವದಲ್ಲಿರಲು ಅಸಂಭವವಾಗಿದೆ. ಜನರೇಟರ್‌ಗಳು ಮತ್ತು ವಿದ್ಯುತ್ ಮೋಟರ್‌ಗಳು, ವಿದ್ಯುತ್ಕಾಂತಗಳು ಮತ್ತು ಟ್ರಾನ್ಸ್‌ಫಾರ್ಮರ್‌ಗಳು, ಅಳತೆ ಉಪಕರಣಗಳು ಮತ್ತು ಹಾಲ್ ಸಂವೇದಕಗಳ ಕಾರ್ಯಾಚರಣೆಯು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಬಳಕೆ ಮತ್ತು ಕಾಂತೀಯ ಹರಿವಿನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಆಧರಿಸಿದೆ.

ಕಾಂತೀಯ ಹರಿವನ್ನು ಕೇಂದ್ರೀಕರಿಸಲು ಮತ್ತು ಬಲಪಡಿಸಲು, ಅವರು ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ವಸ್ತುಗಳ ಬಳಕೆಯನ್ನು ಆಶ್ರಯಿಸುತ್ತಾರೆ. ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ವಸ್ತುಗಳನ್ನು ಉತ್ಪಾದಿಸಲಾಗುತ್ತದೆ ಕಾಂತೀಯ ಕೋರ್ಗಳು - ಅಗತ್ಯವಿರುವ ಆಕಾರಗಳು ಮತ್ತು ಗಾತ್ರಗಳ ದೇಹಗಳು, ಅಗತ್ಯವಿರುವ ದಿಕ್ಕಿನಲ್ಲಿ ಒಂದು ಅಥವಾ ಇನ್ನೊಂದು ಗಾತ್ರದ ಕಾಂತೀಯ ಹರಿವುಗಳನ್ನು ನಿರ್ದೇಶಿಸಲು ಕೋರ್ಗಳು. ಆಯಸ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ಮುಚ್ಚಿದ ರೇಖೆಗಳು ಹಾದುಹೋಗುವ ಅಂತಹ ದೇಹಗಳನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ತಿಳಿದಿರುವ ಗುಣಲಕ್ಷಣಗಳು ವಿವಿಧ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ. ಆದರೆ ಪ್ರಾಯೋಗಿಕ ಕೆಲಸಕ್ಕಾಗಿ, ಈ ಕಾನೂನುಗಳನ್ನು ಪ್ರತಿ ಬಾರಿ ನೇರವಾಗಿ ಬಳಸುವ ಬದಲು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ನಿಯಮಗಳಿಂದ ಪಡೆದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳ ಸಾಮಾನ್ಯ ಪರಿಣಾಮಗಳು ಮತ್ತು ನಿಯಮಗಳಿಗೆ ಆಶ್ರಯಿಸುವುದು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ. ವಿಶಿಷ್ಟವಾದ ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳಿಗೆ ಕೆಲವು ನಿಯಮಗಳನ್ನು ಅನ್ವಯಿಸುವುದು ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ.

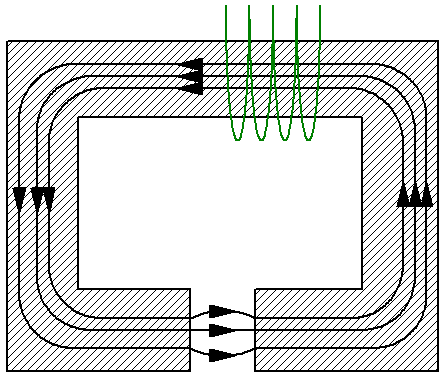
ಉದಾಹರಣೆಗೆ, ಕ್ರಾಸ್-ಸೆಕ್ಷನ್ S ನ ಕವಲೊಡೆದ ನೊಗವನ್ನು ಒಳಗೊಂಡಿರುವ ಸರಳವಾದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಪರಿಗಣಿಸಿ, ಇದು ವಸ್ತುವಿನಿಂದ ಮಾಡಲ್ಪಟ್ಟಿದೆ ಪ್ರವೇಶಸಾಧ್ಯತೆ ಮು… ನೊಗವು ಅದೇ ಪ್ರದೇಶದ S ನ ಕಾಂತೀಯವಲ್ಲದ ಅಂತರವನ್ನು ಹೊಂದಿದೆ, ಉದಾಹರಣೆಗೆ ಗಾಳಿ, ಮತ್ತು ಅಂತರದಲ್ಲಿನ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು - mu1 - ನೊಗದ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯಿಂದ ಭಿನ್ನವಾಗಿದೆ. ಇಲ್ಲಿ ನೀವು ಇಂಡಕ್ಷನ್‌ನ ಸರಾಸರಿ ರೇಖೆಯನ್ನು ನೋಡಬಹುದು ಮತ್ತು ಅದಕ್ಕೆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಟೆನ್ಷನ್ ಪ್ರಮೇಯವನ್ನು ಅನ್ವಯಿಸಬಹುದು:

ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ರೇಖೆಗಳು ಸರ್ಕ್ಯೂಟ್ ಉದ್ದಕ್ಕೂ ನಿರಂತರವಾಗಿರುವುದರಿಂದ, ನೊಗ ಮತ್ತು ಅಂತರ ಎರಡರಲ್ಲೂ ಕಾಂತೀಯ ಹರಿವಿನ ಪ್ರಮಾಣವು ಒಂದೇ ಆಗಿರುತ್ತದೆ. ಈಗ ನಾವು ಸೂತ್ರಗಳನ್ನು ಬಳಸುತ್ತೇವೆ ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಬಿ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಗಾಗಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಪ್ರಕಾರ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ಎಚ್ ಅನ್ನು ವ್ಯಕ್ತಪಡಿಸಲು.

ಮುಂದಿನ ಹಂತವು ಫಲಿತಾಂಶದ ಅಭಿವ್ಯಕ್ತಿಗಳನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಪ್ರಮೇಯದ ಮೇಲಿನ ಸೂತ್ರಕ್ಕೆ ಬದಲಿಸುವುದು:

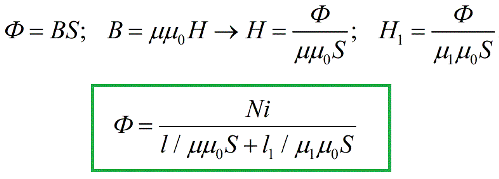
ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್‌ನಲ್ಲಿ ತಿಳಿದಿರುವ ಸೂತ್ರವನ್ನು ನಾವು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ನ ಒಂದು ವಿಭಾಗಕ್ಕೆ ಓಮ್ನ ನಿಯಮ, ಮತ್ತು ಇಲ್ಲಿ EMF ನ ಪಾತ್ರವನ್ನು iN ಪ್ರಮಾಣದಿಂದ ಆಡಲಾಗುತ್ತದೆ, ಇದನ್ನು ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಬಲದೊಂದಿಗೆ ಸಾದೃಶ್ಯದ ಮೂಲಕ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ (ಅಥವಾ MDF) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. SI ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಬಲವನ್ನು ಆಂಪಿಯರ್‌ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ.

ಛೇದದಲ್ಲಿನ ಮೊತ್ತವು ಎಲೆಕ್ಟ್ರಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಒಟ್ಟು ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧದ ಸಾದೃಶ್ಯಕ್ಕಿಂತ ಹೆಚ್ಚೇನೂ ಅಲ್ಲ, ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಅದಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಒಟ್ಟು ಕಾಂತೀಯ ಪ್ರತಿರೋಧ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಛೇದದಲ್ಲಿನ ಪದಗಳು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನ ಪ್ರತ್ಯೇಕ ವಿಭಾಗಗಳ ಕಾಂತೀಯ ಪ್ರತಿರೋಧಗಳಾಗಿವೆ.

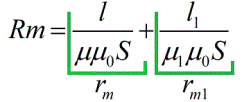
ಮ್ಯಾಗ್ನೆಟಿಕ್ ಪ್ರತಿರೋಧಗಳು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನ ಉದ್ದ, ಅದರ ಅಡ್ಡ-ವಿಭಾಗದ ಪ್ರದೇಶ ಮತ್ತು ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ (ಸಾಮಾನ್ಯ ಓಮ್ನ ನಿಯಮಕ್ಕೆ ವಿದ್ಯುತ್ ವಾಹಕತೆಯನ್ನು ಹೋಲುತ್ತದೆ).ಪರಿಣಾಮವಾಗಿ, ನೀವು ಓಮ್ನ ನಿಯಮದ ಸೂತ್ರವನ್ನು ಬರೆಯಬಹುದು, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಾಗಿ ಮಾತ್ರ:

ಅಂದರೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಓಮ್‌ನ ನಿಯಮದ ಸೂತ್ರೀಕರಣವು ಈ ರೀತಿ ಧ್ವನಿಸುತ್ತದೆ: "ಕವಲೊಡೆಯದೆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಸರ್ಕ್ಯೂಟ್‌ನ ಒಟ್ಟು ಕಾಂತೀಯ ಪ್ರತಿರೋಧದಿಂದ MDS ನ ವಿಭಜನೆಯ ಅಂಶಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ."

ಕಾಂತೀಯ ಪ್ರತಿರೋಧವು ಸೂತ್ರಗಳಿಂದ ಸ್ಪಷ್ಟವಾಗಿದೆ NE ನಲ್ಲಿ ವೆಬರ್ ಆಂಪಿಯರ್‌ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ನ ಒಟ್ಟು ಕಾಂತೀಯ ಪ್ರತಿರೋಧವು ಆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ನ ಭಾಗಗಳ ಕಾಂತೀಯ ಪ್ರತಿರೋಧಗಳ ಮೊತ್ತಕ್ಕೆ ಸಂಖ್ಯಾತ್ಮಕವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ವಿವರಿಸಿದ ಪರಿಸ್ಥಿತಿಯು ಯಾವುದೇ ಸಂಖ್ಯೆಯ ಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಕವಲೊಡೆದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಮಾನ್ಯವಾಗಿರುತ್ತದೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಈ ಎಲ್ಲಾ ಭಾಗಗಳನ್ನು ಅನುಕ್ರಮವಾಗಿ ಭೇದಿಸುತ್ತದೆ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಕೋರ್ಗಳನ್ನು ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಿದರೆ, ಭಾಗಗಳ ಕಾಂತೀಯ ಪ್ರತಿರೋಧಗಳನ್ನು ಸೇರಿಸುವ ಮೂಲಕ ಒಟ್ಟು ಕಾಂತೀಯ ಪ್ರತಿರೋಧವನ್ನು ಕಂಡುಹಿಡಿಯಲಾಗುತ್ತದೆ.

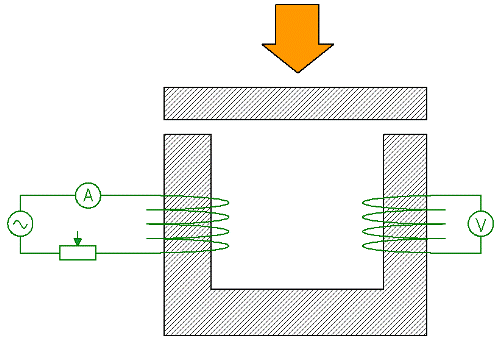
ಸರ್ಕ್ಯೂಟ್‌ನ ಒಟ್ಟು ಹಿಂಜರಿಕೆಯ ಮೇಲೆ ಸರ್ಕ್ಯೂಟ್‌ನ ಭಾಗಗಳ ಹಿಂಜರಿಕೆಯ ಪರಿಣಾಮವನ್ನು ಪ್ರದರ್ಶಿಸುವ ಪ್ರಯೋಗವನ್ನು ಈಗ ಪರಿಗಣಿಸಿ.ಯು-ಆಕಾರದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಕಾಯಿಲ್ 1 ರಿಂದ ಮ್ಯಾಗ್ನೆಟೈಸ್ ಮಾಡಲಾಗುತ್ತದೆ, ಇದು ಆಮ್ಮೀಟರ್ ಮತ್ತು ರಿಯೊಸ್ಟಾಟ್ ಮೂಲಕ ನೀಡಲಾಗುತ್ತದೆ (ಪರ್ಯಾಯ ಪ್ರವಾಹ). ದ್ವಿತೀಯ ಅಂಕುಡೊಂಕಾದ 2 ರಲ್ಲಿ ಇಎಮ್ಎಫ್ ಪ್ರೇರಿತವಾಗಿದೆ ಮತ್ತು ವಿಂಡ್ಗೆ ಸಂಪರ್ಕಗೊಂಡಿರುವ ವೋಲ್ಟ್ಮೀಟರ್ನ ವಾಚನಗೋಷ್ಠಿಗಳು, ನಿಮಗೆ ತಿಳಿದಿರುವಂತೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ಗೆ ಅನುಗುಣವಾಗಿರುತ್ತವೆ.

ನೀವು ಈಗ ಪ್ರಾಥಮಿಕ ಅಂಕುಡೊಂಕಾದ ಪ್ರವಾಹವನ್ನು ರಿಯೊಸ್ಟಾಟ್ನೊಂದಿಗೆ ನಿಯಂತ್ರಿಸುವ ಮೂಲಕ ಬದಲಾಗದೆ ಇರಿಸಿದರೆ ಮತ್ತು ಅದೇ ಸಮಯದಲ್ಲಿ ಮೇಲಿನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನ ವಿರುದ್ಧ ಕಬ್ಬಿಣದ ತಟ್ಟೆಯನ್ನು ಒತ್ತಿದರೆ, ಸರ್ಕ್ಯೂಟ್ನ ಒಟ್ಟು ಕಾಂತೀಯ ಪ್ರತಿರೋಧವು ಬಹಳವಾಗಿ ಕಡಿಮೆಯಾದ ನಂತರ, ಓದುವಿಕೆ ಅದಕ್ಕೆ ಅನುಗುಣವಾಗಿ ವೋಲ್ಟ್ಮೀಟರ್ ಹೆಚ್ಚಾಗುತ್ತದೆ.

ಸಹಜವಾಗಿ, ಮೇಲಿನ ಪದಗಳಾದ "ಮ್ಯಾಗ್ನೆಟೋರೆಸಿಸ್ಟೆನ್ಸ್" ಮತ್ತು "ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್" ಔಪಚಾರಿಕ ಪರಿಕಲ್ಪನೆಗಳಾಗಿವೆ, ಏಕೆಂದರೆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್‌ನಲ್ಲಿ ಏನೂ ಚಲಿಸುವುದಿಲ್ಲ, ಯಾವುದೇ ಚಲಿಸುವ ಕಣಗಳಿಲ್ಲ, ಇದು ಕೇವಲ ಒಂದು ದೃಶ್ಯ ಪ್ರಾತಿನಿಧ್ಯವಾಗಿದೆ (ದ್ರವದ ಹರಿವಿನ ಮಾದರಿಯಂತೆ) ಕಾನೂನುಗಳ ಸ್ಪಷ್ಟ ತಿಳುವಳಿಕೆ...

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಕಾಂತೀಯವಲ್ಲದ ಅಂತರಗಳು ಮತ್ತು ಕಾಂತೀಯ ವಸ್ತುಗಳ ಪರಿಚಯವು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿನ ಕಾಂತೀಯ ಹರಿವಿನ ಮೇಲೆ ಹೇಗೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಎಂಬುದನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಮೇಲಿನ ಪ್ರಯೋಗ ಮತ್ತು ಇತರ ರೀತಿಯ ಪ್ರಯೋಗಗಳ ಭೌತಿಕ ಅರ್ಥವಾಗಿದೆ.

ಉದಾಹರಣೆಗೆ, ಮ್ಯಾಗ್ನೆಟ್ ಅನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗೆ ಪರಿಚಯಿಸುವ ಮೂಲಕ, ನಾವು ಈಗಾಗಲೇ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿರುವ ದೇಹಗಳಿಗೆ ಹೆಚ್ಚುವರಿ ಆಣ್ವಿಕ ಪ್ರವಾಹಗಳನ್ನು ಸೇರಿಸುತ್ತೇವೆ, ಇದು ಹೆಚ್ಚುವರಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ಗಳನ್ನು ಪರಿಚಯಿಸುತ್ತದೆ. ಪ್ರಾಯೋಗಿಕ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸುವಾಗ "ಮ್ಯಾಗ್ನೆಟಿಕ್ ರೆಸಿಸ್ಟೆನ್ಸ್" ಮತ್ತು "ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್" ನಂತಹ ಔಪಚಾರಿಕ ಪರಿಕಲ್ಪನೆಗಳು ತುಂಬಾ ಅನುಕೂಲಕರವೆಂದು ಸಾಬೀತುಪಡಿಸುತ್ತವೆ, ಅದಕ್ಕಾಗಿಯೇ ಅವುಗಳನ್ನು ವಿದ್ಯುತ್ ಎಂಜಿನಿಯರಿಂಗ್ನಲ್ಲಿ ಯಶಸ್ವಿಯಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ.