ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ ಎಂದರೇನು (ಮು)

ಸುರುಳಿಯ ಇಂಡಕ್ಟನ್ಸ್ ಕಾಯಿಲ್ ಇರುವ ಪರಿಸರದ ಗುಣಲಕ್ಷಣಗಳ ಮೇಲೆ ಹೆಚ್ಚು ಅವಲಂಬಿತವಾಗಿದೆ ಎಂದು ಹಲವು ವರ್ಷಗಳ ತಾಂತ್ರಿಕ ಅಭ್ಯಾಸದಿಂದ ನಮಗೆ ತಿಳಿದಿದೆ. ತಿಳಿದಿರುವ ಇಂಡಕ್ಟನ್ಸ್ L0 ನೊಂದಿಗೆ ತಾಮ್ರದ ತಂತಿಯ ಸುರುಳಿಗೆ ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ಕೋರ್ ಅನ್ನು ಸೇರಿಸಿದರೆ, ಇತರ ಹಿಂದಿನ ಸಂದರ್ಭಗಳಲ್ಲಿ ಈ ಸುರುಳಿಯಲ್ಲಿ ಸ್ವಯಂ-ಇಂಡಕ್ಷನ್ ಪ್ರವಾಹಗಳು (ಹೆಚ್ಚುವರಿ ಮುಚ್ಚುವ ಮತ್ತು ತೆರೆಯುವ ಪ್ರವಾಹಗಳು) ಹಲವು ಬಾರಿ ಹೆಚ್ಚಾಗುತ್ತದೆ, ಪ್ರಯೋಗವು ಏನನ್ನು ಸೂಚಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ಖಚಿತಪಡಿಸುತ್ತದೆ. ಹಲವಾರು ಬಾರಿ ಹೆಚ್ಚಾಗುತ್ತದೆ ಇಂಡಕ್ಟನ್ಸ್ಇದು ಈಗ L ಗೆ ಸಮನಾಗಿರುತ್ತದೆ.

ಪ್ರಾಯೋಗಿಕ ವೀಕ್ಷಣೆ

ವಿವರಿಸಿದ ಸುರುಳಿಯ ಒಳಗೆ ಮತ್ತು ಸುತ್ತಲಿನ ಜಾಗವನ್ನು ತುಂಬುವ ಮಾಧ್ಯಮವು ಏಕರೂಪವಾಗಿದೆ ಮತ್ತು ಅದರ ವಾಹಕದ ಮೂಲಕ ಹರಿಯುವ ಪ್ರವಾಹದಿಂದ ಉತ್ಪತ್ತಿಯಾಗುತ್ತದೆ ಎಂದು ನಾವು ಭಾವಿಸೋಣ. ಕಾಂತೀಯ ಕ್ಷೇತ್ರ ಅದರ ಗಡಿಗಳನ್ನು ಮೀರಿ ಹೋಗದೆ ಈ ನಿರ್ದಿಷ್ಟ ಪ್ರದೇಶದಲ್ಲಿ ಮಾತ್ರ ಇದೆ.

ಸುರುಳಿಯು ಟೊರೊಯ್ಡಲ್ ಆಕಾರವನ್ನು ಹೊಂದಿದ್ದರೆ, ಮುಚ್ಚಿದ ಉಂಗುರದ ಆಕಾರವನ್ನು ಹೊಂದಿದ್ದರೆ, ಈ ಮಾಧ್ಯಮವು ಕ್ಷೇತ್ರದೊಂದಿಗೆ ಒಟ್ಟಾಗಿ ಸುರುಳಿಯ ಪರಿಮಾಣದಲ್ಲಿ ಮಾತ್ರ ಕೇಂದ್ರೀಕೃತವಾಗಿರುತ್ತದೆ, ಏಕೆಂದರೆ ಟೊರಾಯ್ಡ್ ಹೊರಗೆ ಪ್ರಾಯೋಗಿಕವಾಗಿ ಯಾವುದೇ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವಿಲ್ಲ.ಈ ಸ್ಥಾನವು ಉದ್ದವಾದ ಸುರುಳಿಗೆ ಸಹ ಮಾನ್ಯವಾಗಿದೆ - ಸೊಲೆನಾಯ್ಡ್, ಇದರಲ್ಲಿ ಎಲ್ಲಾ ಕಾಂತೀಯ ರೇಖೆಗಳು ಸಹ ಒಳಗೆ ಕೇಂದ್ರೀಕೃತವಾಗಿರುತ್ತವೆ - ಅಕ್ಷದ ಉದ್ದಕ್ಕೂ.

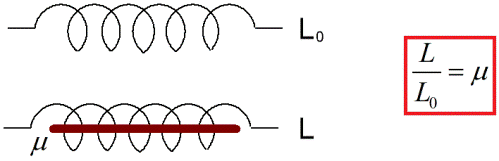
ಉದಾಹರಣೆಗೆ, ನಿರ್ವಾತದಲ್ಲಿ ಕೆಲವು ಸರ್ಕ್ಯೂಟ್ ಅಥವಾ ಕೋರ್ಲೆಸ್ ಕಾಯಿಲ್ನ ಇಂಡಕ್ಟನ್ಸ್ L0 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ನಂತರ ಅದೇ ಸುರುಳಿಗಾಗಿ, ಆದರೆ ಈಗಾಗಲೇ ಕೊಟ್ಟಿರುವ ಸುರುಳಿಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳು ಇರುವ ಜಾಗವನ್ನು ತುಂಬುವ ಏಕರೂಪದ ವಸ್ತುವಿನಲ್ಲಿ, ಇಂಡಕ್ಟನ್ಸ್ L ಆಗಿರಲಿ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, L / L0 ಅನುಪಾತವು ಏನೂ ಅಲ್ಲ ಎಂದು ತಿರುಗುತ್ತದೆ. ನಿರ್ದಿಷ್ಟಪಡಿಸಿದ ವಸ್ತುವಿನ ಸಾಪೇಕ್ಷ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ (ಕೆಲವೊಮ್ಮೆ ಇದನ್ನು "ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ" ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ).

ಇದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ: ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು ನಿರ್ದಿಷ್ಟ ವಸ್ತುವಿನ ಕಾಂತೀಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ನಿರೂಪಿಸುವ ಪ್ರಮಾಣವಾಗಿದೆ. ಸಾಮಾನ್ಯವಾಗಿ ಇದು ವಸ್ತುವಿನ ಸ್ಥಿತಿ (ಮತ್ತು ತಾಪಮಾನ ಮತ್ತು ಒತ್ತಡದಂತಹ ಪರಿಸರ ಪರಿಸ್ಥಿತಿಗಳು) ಮತ್ತು ಅದರ ಸ್ವಭಾವವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.

ಪದವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು

ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿನ ವಸ್ತುವಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ "ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ" ಎಂಬ ಪದದ ಪರಿಚಯವು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದಲ್ಲಿನ ವಸ್ತುವಿಗೆ "ಡೈಎಲೆಕ್ಟ್ರಿಕ್ ಸ್ಥಿರ" ಎಂಬ ಪದದ ಪರಿಚಯಕ್ಕೆ ಹೋಲುತ್ತದೆ.

ಮೇಲಿನ ಸೂತ್ರದ L / L0 ಯಿಂದ ನಿರ್ಧರಿಸಲಾದ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯ ಮೌಲ್ಯವನ್ನು ನಿರ್ದಿಷ್ಟ ವಸ್ತುವಿನ ಸಂಪೂರ್ಣ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ ಮತ್ತು ಸಂಪೂರ್ಣ ಶೂನ್ಯ (ನಿರ್ವಾತ) ಅನುಪಾತವಾಗಿ ವ್ಯಕ್ತಪಡಿಸಬಹುದು.

ಇದನ್ನು ನೋಡುವುದು ಸುಲಭ: ಸಾಪೇಕ್ಷ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ (ಇದನ್ನು ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ) ಆಯಾಮವಿಲ್ಲದ ಪ್ರಮಾಣವಾಗಿದೆ. ಆದರೆ ಸಂಪೂರ್ಣ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು - Hn / m ಆಯಾಮವನ್ನು ಹೊಂದಿದೆ, ನಿರ್ವಾತದ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯಂತೆಯೇ (ಸಂಪೂರ್ಣ!) (ಇದು ಕಾಂತೀಯ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ).

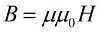
ವಾಸ್ತವವಾಗಿ, ಪರಿಸರ (ಮ್ಯಾಗ್ನೆಟಿಕ್) ಸರ್ಕ್ಯೂಟ್ನ ಇಂಡಕ್ಟನ್ಸ್ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ ಮತ್ತು ಪರಿಸರದಲ್ಲಿನ ಬದಲಾವಣೆಯು ಕಾಂತೀಯ ಹರಿವಿನ ಬದಲಾವಣೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ ಎಂದು ಸ್ಪಷ್ಟವಾಗಿ ತೋರಿಸುತ್ತದೆ Φ ಸರ್ಕ್ಯೂಟ್ಗೆ ಭೇದಿಸುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ ಇಂಡಕ್ಷನ್ ಬಿ ಬದಲಾವಣೆಗೆ ಕಾರಣವಾಗುತ್ತದೆ , ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಪ್ರತಿ ಬಿಂದುವಿಗೆ ಅನ್ವಯಿಸಲಾಗಿದೆ.

ಈ ಅವಲೋಕನದ ಭೌತಿಕ ಅರ್ಥವೇನೆಂದರೆ, ಅದೇ ಸುರುಳಿಯ ಪ್ರವಾಹಕ್ಕೆ (ಅದೇ ಕಾಂತೀಯ ತೀವ್ರತೆಯ H ನಲ್ಲಿ) ಅದರ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಪ್ರಚೋದನೆಯು ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯನ್ನು ಹೊಂದಿರುವ ವಸ್ತುವಿನಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ಪಟ್ಟು ಹೆಚ್ಚು (ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ ಕಡಿಮೆ) ಇರುತ್ತದೆ ಪೂರ್ಣ ನಿರ್ವಾತ.

ಇದು ಈ ರೀತಿ ಏಕೆಂದರೆ ಮಾಧ್ಯಮವನ್ನು ಕಾಂತೀಯಗೊಳಿಸಲಾಗಿದೆ, ಮತ್ತು ಅದು ಸ್ವತಃ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಹೊಂದಲು ಪ್ರಾರಂಭಿಸುತ್ತದೆ.ಈ ರೀತಿಯಲ್ಲಿ ಕಾಂತೀಯಗೊಳಿಸಬಹುದಾದ ಪದಾರ್ಥಗಳನ್ನು ಆಯಸ್ಕಾಂತಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಸಂಪೂರ್ಣ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯ ಮಾಪನದ ಘಟಕವು 1 H / m (ಮೀಟರ್‌ಗೆ ಹೆನ್ರಿ ಅಥವಾ ಪ್ರತಿ ಆಂಪಿಯರ್ ಸ್ಕ್ವೇರ್ಡ್ ನ್ಯೂಟನ್), ಅಂದರೆ, ಇದು ಅಂತಹ ಮಾಧ್ಯಮದ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯಾಗಿದ್ದು, ಅಲ್ಲಿ ಕಾಂತಕ್ಷೇತ್ರದ ವೋಲ್ಟೇಜ್ H 1 A / m , a 1 ರ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ T ಸಂಭವಿಸುತ್ತದೆ.

ವಿದ್ಯಮಾನದ ಭೌತಿಕ ಚಿತ್ರ

ಪ್ರಸ್ತುತ ಲೂಪ್ನ ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಕ್ರಿಯೆಯ ಅಡಿಯಲ್ಲಿ ವಿವಿಧ ವಸ್ತುಗಳು (ಆಯಸ್ಕಾಂತಗಳು) ಕಾಂತೀಯವಾಗುತ್ತವೆ ಮತ್ತು ಪರಿಣಾಮವಾಗಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ, ಇದು ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳ ಮೊತ್ತವಾಗಿದೆ - ಕಾಂತೀಯ ಮಾಧ್ಯಮದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ ಜೊತೆಗೆ ಪ್ರಸ್ತುತ ಲೂಪ್, ಅದಕ್ಕಾಗಿಯೇ ಇದು ಮಧ್ಯಮ ಇಲ್ಲದೆ ಪ್ರಸ್ತುತ-ಮಾತ್ರ ಕ್ಷೇತ್ರ ಸರ್ಕ್ಯೂಟ್‌ಗಳಿಂದ ಪ್ರಮಾಣದಲ್ಲಿ ಭಿನ್ನವಾಗಿರುತ್ತದೆ. ಆಯಸ್ಕಾಂತಗಳ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕಾರಣವು ಅವುಗಳ ಪ್ರತಿಯೊಂದು ಪರಮಾಣುಗಳಲ್ಲಿನ ಚಿಕ್ಕ ಪ್ರವಾಹಗಳ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ.

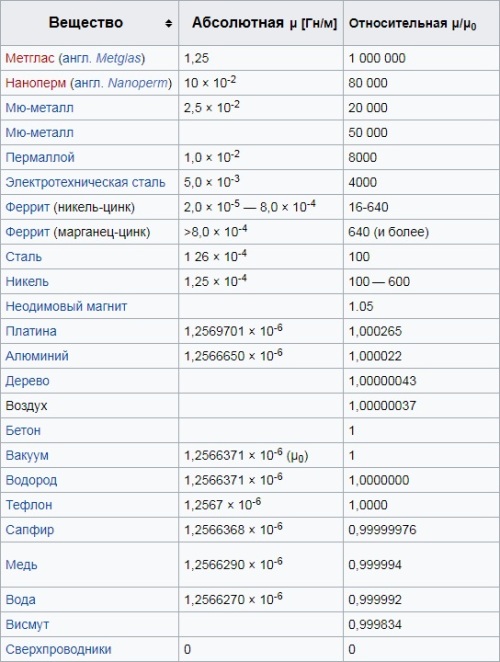
ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯ ಮೌಲ್ಯದ ಪ್ರಕಾರ, ವಸ್ತುಗಳನ್ನು ಡಯಾಮ್ಯಾಗ್ನೆಟಿಕ್ (ಒಂದಕ್ಕಿಂತ ಕಡಿಮೆ - ಅನ್ವಯಿಕ ಕ್ಷೇತ್ರಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಕಾಂತೀಯಗೊಳಿಸಲಾಗಿದೆ), ಪ್ಯಾರಾಮ್ಯಾಗ್ನೆಟ್‌ಗಳು (ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು - ಅನ್ವಯಿಕ ಕ್ಷೇತ್ರದ ದಿಕ್ಕಿನಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟೈಸ್ ಮಾಡಲಾಗಿದೆ) ಮತ್ತು ಫೆರೋಮ್ಯಾಗ್ನೆಟ್‌ಗಳು (ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು - ಅನ್ವಯಿಕ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ನಿಷ್ಕ್ರಿಯಗೊಳಿಸಿದ ನಂತರ ಕಾಂತೀಯಗೊಳಿಸಲಾಗಿದೆ ಮತ್ತು ಕಾಂತೀಕರಣವನ್ನು ಹೊಂದಿದೆ).

ಫೆರೋಮ್ಯಾಗ್ನೆಟ್‌ಗಳನ್ನು ಇವುಗಳಿಂದ ನಿರೂಪಿಸಲಾಗಿದೆ ಹಿಸ್ಟರೆಸಿಸ್ಆದ್ದರಿಂದ, ಅದರ ಶುದ್ಧ ರೂಪದಲ್ಲಿ "ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯ" ಪರಿಕಲ್ಪನೆಯು ಫೆರೋಮ್ಯಾಗ್ನೆಟ್ಗಳಿಗೆ ಅನ್ವಯಿಸುವುದಿಲ್ಲ, ಆದರೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಶ್ರೇಣಿಯ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ನಲ್ಲಿ, ಕೆಲವು ಅಂದಾಜಿನಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕರ್ವ್ನ ರೇಖೀಯ ಭಾಗವನ್ನು ಪ್ರತ್ಯೇಕಿಸಬಹುದು, ಇದಕ್ಕಾಗಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸಾಧ್ಯವಾಗುತ್ತದೆ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ.

ಸೂಪರ್ ಕಂಡಕ್ಟರ್‌ಗಳಲ್ಲಿ, ಆಯಸ್ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು 0 ಆಗಿರುತ್ತದೆ (ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಅವುಗಳ ಪರಿಮಾಣದಿಂದ ಸಂಪೂರ್ಣವಾಗಿ ಸ್ಥಳಾಂತರಗೊಂಡಿರುವುದರಿಂದ), ಮತ್ತು ಗಾಳಿಯ ಸಂಪೂರ್ಣ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು ಮು ನಿರ್ವಾತಕ್ಕೆ ಬಹುತೇಕ ಸಮಾನವಾಗಿರುತ್ತದೆ (ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕವನ್ನು ಓದಿ). ಗಾಳಿಗಾಗಿ, mu 1 ಕ್ಕಿಂತ ಸ್ವಲ್ಪ ಹೆಚ್ಚು.