ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳನ್ನು ಅಳೆಯುವ ತತ್ವಗಳು, ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ನಿಯತಾಂಕಗಳನ್ನು ಅಳೆಯುವ ಉಪಕರಣಗಳು

ಭೂಮಿಯ ಆಯಸ್ಕಾಂತೀಯ ಧ್ರುವಗಳಿಗೆ ದಿಕ್ಕುಗಳನ್ನು ಸೂಚಿಸುವ ಮೊದಲ ಕಾಂತೀಯ ದಿಕ್ಸೂಚಿಗಳು BC ಮೂರನೇ ಶತಮಾನದಲ್ಲಿ ಚೀನಾದಲ್ಲಿ ಕಾಣಿಸಿಕೊಂಡವು. ಇವುಗಳು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಕಬ್ಬಿಣದ ಅದಿರಿನಿಂದ ಮಾಡಿದ ಶಾರ್ಟ್-ಹ್ಯಾಂಡ್ಡ್ ರೌಂಡ್ ಲ್ಯಾಡಲ್ಗಳ ರೂಪದಲ್ಲಿ ಸಾಧನಗಳಾಗಿವೆ.

ಚಮಚವನ್ನು ಅದರ ಪೀನ ಭಾಗದೊಂದಿಗೆ ನಯವಾದ ತಾಮ್ರ ಅಥವಾ ಮರದ ಮೇಲ್ಮೈಯಲ್ಲಿ ಇರಿಸಲಾಯಿತು, ಅದರ ಮೇಲೆ ರಾಶಿಚಕ್ರದ ಚಿಹ್ನೆಗಳ ಚಿತ್ರಗಳೊಂದಿಗೆ ವಿಭಾಗಗಳನ್ನು ಚಿತ್ರಿಸಲಾಗಿದೆ, ಇದು ಕಾರ್ಡಿನಲ್ ಬಿಂದುಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ. ದಿಕ್ಸೂಚಿಯನ್ನು ಸಕ್ರಿಯಗೊಳಿಸಲು, ಚಮಚವನ್ನು ಲಘುವಾಗಿ ಒತ್ತಿದರೆ ಮತ್ತು ಅದು ತಿರುಗಲು ಪ್ರಾರಂಭಿಸಿತು. ಅಂತಿಮವಾಗಿ, ಚಮಚವನ್ನು ನಿಲ್ಲಿಸಿದಾಗ, ಅದರ ಹಿಡಿಕೆಯನ್ನು ಸರಿಯಾಗಿ ತೋರಿಸಲಾಯಿತು ಭೂಮಿಯ ದಕ್ಷಿಣ ಕಾಂತೀಯ ಧ್ರುವದ ಕಡೆಗೆ.

ಹನ್ನೆರಡನೆಯ ಶತಮಾನದಿಂದ, ದಿಕ್ಸೂಚಿಗಳನ್ನು ಯುರೋಪ್ನಲ್ಲಿ ಪ್ರಯಾಣಿಕರು ಸಕ್ರಿಯವಾಗಿ ಬಳಸುತ್ತಿದ್ದರು. ಕಾಂತೀಯ ವಿಚಲನವನ್ನು ನಿರ್ಧರಿಸಲು ಭೂ ಸಾರಿಗೆ ಮತ್ತು ಸಮುದ್ರ ಹಡಗುಗಳೆರಡರಲ್ಲೂ ಅವುಗಳನ್ನು ಸ್ಥಾಪಿಸಲಾಗಿದೆ.

ಹದಿನೆಂಟನೇ ಶತಮಾನದ ಅಂತ್ಯದಿಂದ, ಕಾಂತೀಯ ವಿದ್ಯಮಾನಗಳು ಆ ಕಾಲದ ವಿಜ್ಞಾನಿಗಳಿಗೆ ಎಚ್ಚರಿಕೆಯಿಂದ ಅಧ್ಯಯನದ ವಸ್ತುವಾಯಿತು. 1785 ರಲ್ಲಿ ಪೆಂಡೆಂಟ್ ಭೂಮಿಯ ಕಾಂತಕ್ಷೇತ್ರದ ಬಲವನ್ನು ಪ್ರಮಾಣೀಕರಿಸುವ ವಿಧಾನವನ್ನು ಪ್ರಸ್ತಾಪಿಸಿದರು. 1832 ರಲ್ಲಿಹೆಚ್ಚು ನಿಖರವಾದ ಮಾಪನಗಳ ಮೂಲಕ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಬಲದ ಸಂಪೂರ್ಣ ಮೌಲ್ಯವನ್ನು ನಿರ್ಧರಿಸುವ ಸಾಧ್ಯತೆಯನ್ನು ಗಾಸ್ ತೋರಿಸಿದರು.

ವಿದ್ಯುದಾವೇಶಗಳ ಚಲನೆಯ ಸಮಯದಲ್ಲಿ ಕಂಡುಬರುವ ಕಾಂತೀಯ ವಿದ್ಯಮಾನಗಳು ಮತ್ತು ಬಲ ಪರಿಣಾಮಗಳ ನಡುವಿನ ಸಂಪರ್ಕವನ್ನು ಮೊದಲು 1820 ರಲ್ಲಿ ಓರ್ಸ್ಟೆಡ್ ಸ್ಥಾಪಿಸಿದರು. ಮ್ಯಾಕ್ಸ್‌ವೆಲ್ ನಂತರ ಈ ಸಂಬಂಧವನ್ನು ತರ್ಕಬದ್ಧ ರೂಪದಲ್ಲಿ ಬರೆಯುತ್ತಾರೆ- ಗಣಿತದ ಸಮೀಕರಣಗಳ ರೂಪದಲ್ಲಿ (1873):

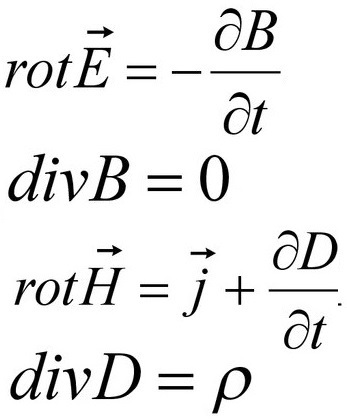
ಇಲ್ಲಿಯವರೆಗೆ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ನಿಯತಾಂಕಗಳನ್ನು ಅಳೆಯಲು ಈ ಕೆಳಗಿನ ತಂತ್ರವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ:

• ಟೆಸ್ಲಾಮೀಟರ್ಗಳು - ಬಲ H ಅಥವಾ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ B ಯ ಇಂಡಕ್ಷನ್ ಮೌಲ್ಯಗಳನ್ನು ಅಳೆಯುವ ಸಾಧನಗಳು;

• ವೆಬ್ಮೀಟರ್ಗಳು - ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ Ф ಪ್ರಮಾಣವನ್ನು ಅಳೆಯುವ ಉಪಕರಣಗಳು;

• ಗ್ರೇಡಿಯೋಮೀಟರ್ಗಳು - ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಅಸಮಂಜಸತೆಯನ್ನು ಅಳೆಯುವ ಸಾಧನಗಳು.

ಸಹ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ:

• ಕಾಂತೀಯ ಕ್ಷಣವನ್ನು ಅಳೆಯುವ ಸಾಧನಗಳು M;

• ವೆಕ್ಟರ್ ಬಿ ದಿಕ್ಕನ್ನು ಅಳೆಯುವ ಉಪಕರಣಗಳು;

• ವಿವಿಧ ವಸ್ತುಗಳ ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕಗಳನ್ನು ಅಳೆಯುವ ಉಪಕರಣಗಳು.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ B ಬಲವಾದ ಅಡ್ಡ ಕ್ರಿಯೆಯ ತೀವ್ರತೆಯನ್ನು ನಿರೂಪಿಸುತ್ತದೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರ (ಧ್ರುವಕ್ಕೆ ಅಥವಾ ಪ್ರವಾಹಕ್ಕೆ) ಮತ್ತು ಆದ್ದರಿಂದ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಅದರ ಮುಖ್ಯ ಲಕ್ಷಣವಾಗಿದೆ.

ಹೀಗಾಗಿ, ಅಧ್ಯಯನದ ಅಡಿಯಲ್ಲಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಒಂದು ಮ್ಯಾಗ್ನೆಟ್ ಅಥವಾ ಪ್ರಸ್ತುತ ಅಂಶದೊಂದಿಗೆ ಬಲವಾಗಿ ಸಂವಹನ ನಡೆಸಬಹುದು ಮತ್ತು ಸರ್ಕ್ಯೂಟ್‌ಗೆ ಭೇದಿಸುವ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಕಾಲಾನಂತರದಲ್ಲಿ ಬದಲಾದರೆ ಅಥವಾ ಸರ್ಕ್ಯೂಟ್‌ನ ಸ್ಥಾನವನ್ನು ಬದಲಾಯಿಸಿದರೆ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಇಂಡಕ್ಷನ್ ಇಎಮ್‌ಎಫ್ ಅನ್ನು ಪ್ರೇರೇಪಿಸುವ ಸಾಮರ್ಥ್ಯವನ್ನು ಹೊಂದಿದೆ. ಕಾಂತೀಯ ಕ್ಷೇತ್ರ.

ಇಂಡಕ್ಷನ್ B ಯ ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ dl ಉದ್ದದ ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ಅಂಶವು F ಬಲದಿಂದ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಅದರ ಮೌಲ್ಯವನ್ನು ಈ ಕೆಳಗಿನ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಕಂಡುಹಿಡಿಯಬಹುದು:

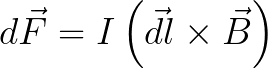
ಆದ್ದರಿಂದ, ಅಧ್ಯಯನ ಮಾಡಿದ ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ ಬಿ ಅನ್ನು ಎಫ್ ಬಲದಿಂದ ಕಂಡುಹಿಡಿಯಬಹುದು, ಇದು ನಿರ್ದಿಷ್ಟ ಉದ್ದದ ವಾಹಕದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ l, ತಿಳಿದಿರುವ ಮೌಲ್ಯ I ನ ನೇರ ಪ್ರವಾಹದೊಂದಿಗೆ ಈ ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಲಾಗುತ್ತದೆ.

ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಕ್ಷಣ ಎಂದು ಕರೆಯಲ್ಪಡುವ ಪ್ರಮಾಣವನ್ನು ಬಳಸಿಕೊಂಡು ಕಾಂತೀಯ ಮಾಪನಗಳನ್ನು ಅನುಕೂಲಕರವಾಗಿ ನಿರ್ವಹಿಸಲಾಗುತ್ತದೆ. ಕಾಂತೀಯ ಕ್ಷಣ Pm ಪ್ರಸ್ತುತ I ನೊಂದಿಗೆ S ಪ್ರದೇಶದ ಬಾಹ್ಯರೇಖೆಯನ್ನು ನಿರೂಪಿಸುತ್ತದೆ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷಣದ ಪ್ರಮಾಣವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

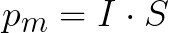
N ತಿರುವುಗಳನ್ನು ಹೊಂದಿರುವ ಸುರುಳಿಯನ್ನು ಬಳಸಿದರೆ, ಅದರ ಕಾಂತೀಯ ಕ್ಷಣವು ಇದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

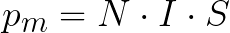
ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಟರಾಕ್ಷನ್ ಫೋರ್ಸ್ನ ಯಾಂತ್ರಿಕ ಕ್ಷಣ M ಅನ್ನು ಕಾಂತೀಯ ಕ್ಷಣ Pm ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ B ಯ ಮೌಲ್ಯಗಳ ಆಧಾರದ ಮೇಲೆ ಈ ಕೆಳಗಿನಂತೆ ಕಂಡುಹಿಡಿಯಬಹುದು:

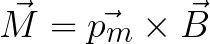
ಆದಾಗ್ಯೂ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಅಳೆಯಲು, ಯಾಂತ್ರಿಕ ಬಲದ ಅದರ ಅಭಿವ್ಯಕ್ತಿಗಳನ್ನು ಬಳಸಲು ಯಾವಾಗಲೂ ಅನುಕೂಲಕರವಾಗಿರುವುದಿಲ್ಲ. ಅದೃಷ್ಟವಶಾತ್, ನೀವು ನಂಬಬಹುದಾದ ಮತ್ತೊಂದು ವಿದ್ಯಮಾನವಿದೆ. ಇದು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವಿದ್ಯಮಾನವಾಗಿದೆ. ಗಣಿತದ ರೂಪದಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ನಿಯಮವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಬರೆಯಲಾಗಿದೆ:

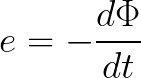
ಹೀಗಾಗಿ, ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಪಡೆಗಳು ಅಥವಾ ಪ್ರೇರಿತ ಇಎಮ್ಎಫ್ ಆಗಿ ಸ್ವತಃ ಪ್ರಕಟವಾಗುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಮೂಲವು ತಿಳಿದಿರುವಂತೆ, ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿದೆ.

ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಉತ್ಪಾದಿಸುವ ಪ್ರಸ್ತುತವು ತಿಳಿದಿದ್ದರೆ, ಆ ಹಂತದಲ್ಲಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಬಲವನ್ನು (ಪ್ರಸ್ತುತ ಅಂಶದಿಂದ r ದೂರದಲ್ಲಿ) ಕಂಡುಹಿಡಿಯಬಹುದು. ಬಯೋಟ್-ಸಾವರ್ಟ್-ಲ್ಯಾಪ್ಲೇಸ್ ಕಾನೂನನ್ನು ಬಳಸುವುದು:

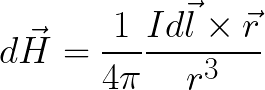
ನಿರ್ವಾತದಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ B ಈ ಕೆಳಗಿನ ಸಂಬಂಧದಿಂದ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ H (ಅನುಗುಣವಾದ ಪ್ರವಾಹದಿಂದ ಉತ್ಪತ್ತಿಯಾಗುತ್ತದೆ) ಗೆ ಸಂಬಂಧಿಸಿದೆ ಎಂದು ಗಮನಿಸಬೇಕು:

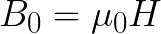
SI ವ್ಯವಸ್ಥೆಯಲ್ಲಿನ ನಿರ್ವಾತ ಕಾಂತೀಯ ಸ್ಥಿರಾಂಕವನ್ನು ಆಂಪಿಯರ್‌ಗಳಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.ಅನಿಯಂತ್ರಿತ ಮಾಧ್ಯಮಕ್ಕೆ, ಈ ಸ್ಥಿರಾಂಕವು ನಿರ್ವಾತದಲ್ಲಿನ ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್‌ಗೆ ನಿರ್ದಿಷ್ಟ ಮಾಧ್ಯಮದಲ್ಲಿನ ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ಅನುಪಾತವಾಗಿದೆ ಮತ್ತು ಈ ಸ್ಥಿರವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮಾಧ್ಯಮದ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ:

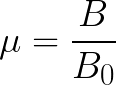
ಗಾಳಿಯ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯು ಪ್ರಾಯೋಗಿಕವಾಗಿ ನಿರ್ವಾತದ ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯೊಂದಿಗೆ ಸೇರಿಕೊಳ್ಳುತ್ತದೆ; ಆದ್ದರಿಂದ, ಗಾಳಿಗಾಗಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ B ಪ್ರಾಯೋಗಿಕವಾಗಿ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಒತ್ತಡ H ಗೆ ಹೋಲುತ್ತದೆ.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಅನ್ನು ಅಳೆಯುವ ಘಟಕ NE ನಲ್ಲಿ - ಟೆಸ್ಲಾ [T], CGS ವ್ಯವಸ್ಥೆಯಲ್ಲಿ - ಗಾಸ್ [G], ಮತ್ತು 1 T = 10000 G. ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ ಅನ್ನು ನಿರ್ಧರಿಸಲು ಅಳತೆ ಮಾಡುವ ಸಾಧನಗಳನ್ನು ಟೆಸ್ಲಾಮೀಟರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ H ಅನ್ನು ಪ್ರತಿ ಮೀಟರ್‌ಗೆ (A/m) ಆಂಪಿಯರ್‌ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ, 1 ಆಂಪಿಯರ್/ಮೀಟರ್ ಅನ್ನು 1 ಆಂಪಿಯರ್ ಸೊಲೀನಾಯ್ಡ್ ಪ್ರವಾಹವು ಅದರ ಮೂಲಕ ಹರಿಯುವಾಗ ಘಟಕ ತಿರುವು ಸಾಂದ್ರತೆಯ ಅನಂತ ಉದ್ದದ ಸೊಲೀನಾಯ್ಡ್‌ನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ಪ್ರತಿ ಮೀಟರ್ಗೆ ಒಂದು ಆಂಪಿಯರ್ ಅನ್ನು ಇನ್ನೊಂದು ರೀತಿಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು: ಇದು 1 ಮೀಟರ್ನ ಲೂಪ್ ವ್ಯಾಸದೊಂದಿಗೆ 1 ಆಂಪಿಯರ್ನ ಪ್ರವಾಹದೊಂದಿಗೆ ವೃತ್ತಾಕಾರದ ಸರ್ಕ್ಯೂಟ್ನ ಮಧ್ಯಭಾಗದಲ್ಲಿರುವ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯಾಗಿದೆ.

ಇಲ್ಲಿ ಇಂಡಕ್ಷನ್ನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನಂತಹ ಮೌಲ್ಯವನ್ನು ಗಮನಿಸುವುದು ಯೋಗ್ಯವಾಗಿದೆ - ಎಫ್. ಇದು ಸ್ಕೇಲಾರ್ ಪ್ರಮಾಣವಾಗಿದೆ, SI ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಇದನ್ನು ವೆಬರ್ಸ್ನಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ ಮತ್ತು CGS ವ್ಯವಸ್ಥೆಯಲ್ಲಿ - ಮ್ಯಾಕ್ಸ್ವೆಲ್ಸ್ನಲ್ಲಿ 1 μs = 0.00000001 Wb. 1 ವೆಬರ್ ಅಂತಹ ಪ್ರಮಾಣದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಆಗಿದ್ದು ಅದು ಶೂನ್ಯಕ್ಕೆ ಕಡಿಮೆಯಾದಾಗ, 1-ಕೂಲಮ್ ಚಾರ್ಜ್ 1 ಓಮ್ನ ಪ್ರತಿರೋಧದೊಂದಿಗೆ ವಾಹಕ ಸರ್ಕ್ಯೂಟ್ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ.

ನಾವು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಅನ್ನು ಆರಂಭಿಕ ಮೌಲ್ಯವಾಗಿ ತೆಗೆದುಕೊಂಡರೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫೀಲ್ಡ್ ಇಂಡಕ್ಷನ್ ಬಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಸಾಂದ್ರತೆಗಿಂತ ಹೆಚ್ಚೇನೂ ಆಗಿರುವುದಿಲ್ಲ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ಅಳೆಯುವ ಸಾಧನಗಳನ್ನು ವೆಬ್ಮೀಟರ್ಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಅನ್ನು ಬಲದಿಂದ (ಅಥವಾ ಯಾಂತ್ರಿಕ ಕ್ಷಣದಿಂದ) ಅಥವಾ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ಪ್ರೇರಿತವಾದ ಇಎಮ್‌ಎಫ್‌ನಿಂದ ನಿರ್ಧರಿಸಬಹುದು ಎಂದು ನಾವು ಮೇಲೆ ಗಮನಿಸಿದ್ದೇವೆ. ಇವುಗಳು ನೇರ ಮಾಪನ ಪರಿವರ್ತನೆಗಳು ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತವೆ, ಅಲ್ಲಿ ಕಾಂತೀಯ ಹರಿವು ಅಥವಾ ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಅನ್ನು ಮತ್ತೊಂದು ಭೌತಿಕ ಪ್ರಮಾಣದಿಂದ (ಬಲ, ಚಾರ್ಜ್, ಕ್ಷಣ, ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸ) ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ, ಇದು ಮೂಲಭೂತ ಭೌತಿಕ ಕಾನೂನಿನ ಮೂಲಕ ಕಾಂತೀಯ ಪ್ರಮಾಣಕ್ಕೆ ಅನನ್ಯವಾಗಿ ಸಂಬಂಧಿಸಿದೆ.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಬಿ ಅಥವಾ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಪ್ರಸ್ತುತ I ಅಥವಾ ಉದ್ದ l ಅಥವಾ ತ್ರಿಜ್ಯ r ಮೂಲಕ ಇರುವ ರೂಪಾಂತರಗಳನ್ನು ಹಿಮ್ಮುಖ ರೂಪಾಂತರಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅಂತಹ ರೂಪಾಂತರಗಳನ್ನು ಬಯೋಟ್-ಸಾವರ್ಟ್-ಲ್ಯಾಪ್ಲೇಸ್ ಕಾನೂನಿನ ಆಧಾರದ ಮೇಲೆ ನಡೆಸಲಾಗುತ್ತದೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಬಿ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ನಡುವಿನ ತಿಳಿದಿರುವ ಸಂಬಂಧವನ್ನು ಬಳಸಿ.