ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳ ಲೆಕ್ಕಾಚಾರಗಳು

ವಿದ್ಯುತ್ ಯಂತ್ರಗಳು ಮತ್ತು ಉಪಕರಣಗಳಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ (ಫೆರೋಮ್ಯಾಗ್ನೆಟಿಕ್ ಕೋರ್) ಮತ್ತು ಈ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನ ಗಾಳಿಯ ಅಂತರದಲ್ಲಿ ಕೇಂದ್ರೀಕೃತವಾಗಿರುತ್ತದೆ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನ ಈ ಮಾರ್ಗವನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನಂತಿದೆ. ಕಾಂತೀಯ ಹರಿವು Ф ವಿದ್ಯುತ್ ಪ್ರವಾಹ I ಅನ್ನು ಹೋಲುತ್ತದೆ, ಇಂಡಕ್ಷನ್ В ಪ್ರಸ್ತುತ ಸಾಂದ್ರತೆಯನ್ನು ಹೋಲುತ್ತದೆ, ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಫೋರ್ಸ್ (ns) FN (H ∙ l = I ∙ ω) e ಗೆ ಅನುರೂಪವಾಗಿದೆ. ಇತ್ಯಾದಿ ಜೊತೆಗೆ

ಸರಳವಾದ ಸಂದರ್ಭದಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಎಲ್ಲೆಡೆ ಒಂದೇ ಅಡ್ಡ-ವಿಭಾಗವನ್ನು ಹೊಂದಿದೆ ಮತ್ತು ಏಕರೂಪದ ಕಾಂತೀಯ ವಸ್ತುಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟಿದೆ. ಎನ್ ನಿರ್ಧರಿಸಲು. ಅಗತ್ಯವಿರುವ ಇಂಡಕ್ಷನ್ B ಅನ್ನು ಒದಗಿಸಲು l ∙ ω ಜೊತೆಗೆ, ಅನುಗುಣವಾದ ತೀವ್ರತೆಯನ್ನು H ಅನ್ನು ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕರ್ವ್‌ನಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಯ ಸರಾಸರಿ ಉದ್ದದಿಂದ ಗುಣಿಸಲಾಗುತ್ತದೆ l: H ∙ l = I ∙ ω = Fm.

ಇಲ್ಲಿಂದ, ಅಗತ್ಯವಿರುವ ಪ್ರಸ್ತುತ I ಅಥವಾ ಸುರುಳಿಯ ತಿರುವುಗಳ ಸಂಖ್ಯೆ ω ಅನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ಸಂಕೀರ್ಣ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಸಾಮಾನ್ಯವಾಗಿ ವಿವಿಧ ವಿಭಾಗಗಳು ಮತ್ತು ಕಾಂತೀಯ ವಸ್ತುಗಳೊಂದಿಗೆ ವಿಭಾಗಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಈ ವಿಭಾಗಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಿಸಲಾಗುತ್ತದೆ, ಆದ್ದರಿಂದ ಅದೇ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದರ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ.ಪ್ರತಿ ವಿಭಾಗದಲ್ಲಿನ ಇಂಡಕ್ಷನ್ ಬಿ ವಿಭಾಗದ ಅಡ್ಡ-ವಿಭಾಗವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ ಮತ್ತು ಪ್ರತಿ ವಿಭಾಗಕ್ಕೆ ಪ್ರತ್ಯೇಕವಾಗಿ B = Φ∶S ಸೂತ್ರದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ.

ಇಂಡಕ್ಷನ್ನ ವಿಭಿನ್ನ ಮೌಲ್ಯಗಳಿಗೆ, ಕಾಂತೀಯೀಕರಣದ ಕರ್ವ್ನಿಂದ ತೀವ್ರತೆಯನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಸರ್ಕ್ಯೂಟ್ನ ಅನುಗುಣವಾದ ವಿಭಾಗದ ವಿದ್ಯುತ್ ಲೈನ್ನ ಸರಾಸರಿ ಉದ್ದದಿಂದ ಗುಣಿಸಲಾಗುತ್ತದೆ. ವೈಯಕ್ತಿಕ ಕೃತಿಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿ, ಒಬ್ಬರು ಸಂಪೂರ್ಣ n ಅನ್ನು ಪಡೆಯುತ್ತಾರೆ. c. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 +… ಇದು ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಕರೆಂಟ್ ಅಥವಾ ಕಾಯಿಲ್ ತಿರುವುಗಳ ಸಂಖ್ಯೆಯನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ.

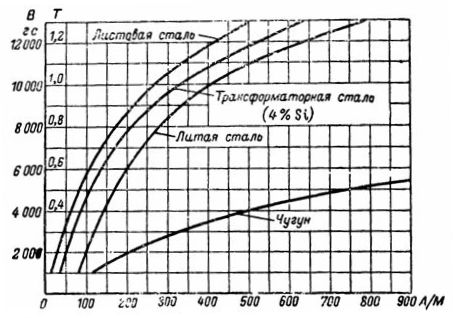
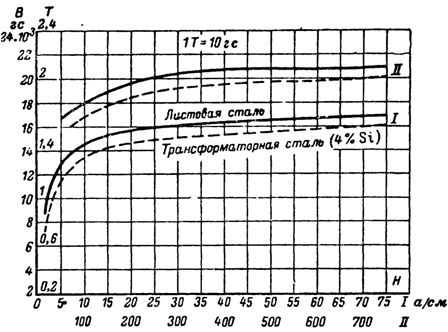
ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ವಕ್ರಾಕೃತಿಗಳು

ಉದಾಹರಣೆಗಳು

1. 200 ತಿರುವುಗಳ ಸುರುಳಿಯ ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಕರೆಂಟ್ I ಏನಾಗಿರಬೇಕು ಆದ್ದರಿಂದ n. c. ಎರಕಹೊಯ್ದ ಕಬ್ಬಿಣದ ಉಂಗುರದಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ Ф = 15700 Ms = 0.000157 Wb ಅನ್ನು ರಚಿಸಲಾಗಿದೆ? ಎರಕಹೊಯ್ದ ಕಬ್ಬಿಣದ ಉಂಗುರದ ಸರಾಸರಿ ತ್ರಿಜ್ಯವು r = 5 cm, ಮತ್ತು ಅದರ ವಿಭಾಗದ ವ್ಯಾಸವು d = 2 cm (Fig. 1).

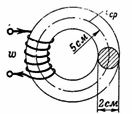
ಅಕ್ಕಿ. 1.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ S = (π ∙ d ^ 2) / 4 = 3.14 cm2 ನ ವಿಭಾಗ.

ಕೋರ್ನಲ್ಲಿನ ಇಂಡಕ್ಷನ್: B = Φ∶S = 15700∶3.14 = 5000 G.

MKSA ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಇಂಡಕ್ಷನ್: B = 0.000157 Wb: 0.0000314 m2 = 0.5 T.

ಎರಕಹೊಯ್ದ ಕಬ್ಬಿಣದ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕರ್ವ್ನಿಂದ, ನಾವು B = 5000 G = 0.5 T ಗೆ 750 A / m ಗೆ ಸಮಾನವಾದ ಅಗತ್ಯವಿರುವ ಶಕ್ತಿ H ಅನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ. ಕಾಂತೀಯಗೊಳಿಸುವ ಸಾಮರ್ಥ್ಯವು ಇದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ: I ∙ ω = H ∙ l = 235.5 Av.

ಆದ್ದರಿಂದ, ಅಗತ್ಯವಿರುವ ಪ್ರಸ್ತುತ I = (H ∙ l) / ω = 235.5 / 200 = 1.17 ಎ.

2. ಮುಚ್ಚಿದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ (ಚಿತ್ರ 2) ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ಉಕ್ಕಿನ ಫಲಕಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟಿದೆ. ಕೋರ್ Ф = 160000 Ms = 0.0016 Wb ನಲ್ಲಿ ಕಾಂತೀಯ ಹರಿವನ್ನು ರಚಿಸಲು 0.5 A ಪ್ರವಾಹದೊಂದಿಗೆ ಸುರುಳಿಯಲ್ಲಿ ಎಷ್ಟು ತಿರುವುಗಳು ಇರಬೇಕು?

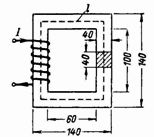
ಅಕ್ಕಿ. 2.

ಕೋರ್ ವಿಭಾಗ S = 4 ∙ 4 = 16 cm2 = 0.0016 m2.

ಕೋರ್ ಇಂಡಕ್ಷನ್ ಬಿ = ಎಫ್ / ಎಸ್ = 160000/16 = 10000 ಜಿಎಸ್ = 1 ಟಿ.

ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ ಸ್ಟೀಲ್ನ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕರ್ವ್ ಪ್ರಕಾರ, ನಾವು B = 10,000 Gs = 1 T ಗಾಗಿ H = 3.25 A / cm = 325 A / m ತೀವ್ರತೆಯನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ.

ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಯ ಸರಾಸರಿ ಉದ್ದವು l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0.48 ಮೀ.

ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಫೋರ್ಸ್ Fm = I ∙ ω = H ∙ l = 3.25 ∙ 48 = 315 ∙ 0.48 = 156 Av.

0.5 ಎ ಪ್ರವಾಹದಲ್ಲಿ, ತಿರುವುಗಳ ಸಂಖ್ಯೆ ω = 156 / 0.5 = 312 ಆಗಿದೆ.

3. ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಿರುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್. 3 ಹಿಂದಿನ ಉದಾಹರಣೆಯ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಹೋಲುತ್ತದೆ, ಅದು δ = 5 ಮಿಮೀ ಗಾಳಿಯ ಅಂತರವನ್ನು ಹೊಂದಿದೆ. ಎನ್ ಏನಾಗಿರಬೇಕು. s. ಮತ್ತು ಕಾಯಿಲ್ ಕರೆಂಟ್ ಆದ್ದರಿಂದ ಕಾಂತೀಯ ಹರಿವು ಹಿಂದಿನ ಉದಾಹರಣೆಯಂತೆಯೇ ಇರುತ್ತದೆ, ಅಂದರೆ F = 160000 Ms = 0.0016 Wb?

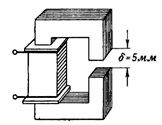
ಅಕ್ಕಿ. 3.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಎರಡು ಸರಣಿ-ಸಂಪರ್ಕಿತ ವಿಭಾಗಗಳನ್ನು ಹೊಂದಿದೆ, ಅದರ ಅಡ್ಡ-ವಿಭಾಗವು ಹಿಂದಿನ ಉದಾಹರಣೆಯಂತೆಯೇ ಇರುತ್ತದೆ, ಅಂದರೆ S = 16 cm2. ಇಂಡಕ್ಟನ್ಸ್ ಸಹ B = 10000 G = 1 T ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಉಕ್ಕಿನ ಕಾಂತೀಯ ರೇಖೆಯ ಸರಾಸರಿ ಉದ್ದವು ಸ್ವಲ್ಪ ಚಿಕ್ಕದಾಗಿದೆ: lс = 48-0.5 = 47.5 cm ≈0.48 m.

ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನ ಈ ವಿಭಾಗದಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ವೋಲ್ಟೇಜ್ Hc ∙ lc = 3.25 ∙ 48≈156 Av.

ಗಾಳಿಯ ಅಂತರದಲ್ಲಿ ಕ್ಷೇತ್ರದ ಸಾಮರ್ಥ್ಯ: Hδ = 0.8 ∙ B = 0.8 ∙ 10000 = 8000 A / cm.

ಗಾಳಿಯ ಅಂತರದ ಅಡ್ಡ-ವಿಭಾಗದಲ್ಲಿ ಕಾಂತೀಯ ಒತ್ತಡ Hδ ∙ δ = 8000 ∙ 0.5 = 4000 Av.

ಸಂಪೂರ್ಣ ಎನ್. c. ಪ್ರತ್ಯೇಕ ವಿಭಾಗಗಳಲ್ಲಿನ ಕಾಂತೀಯ ವೋಲ್ಟೇಜ್ಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13.3 ಎ.

ಹಿಂದಿನ ಉದಾಹರಣೆಯಲ್ಲಿ ಅಗತ್ಯವಾದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು 0.5 ಎ ಪ್ರವಾಹದಿಂದ ಒದಗಿಸಿದ್ದರೆ, 0.5 ಸೆಂ.ಮೀ ಗಾಳಿಯ ಅಂತರವನ್ನು ಹೊಂದಿರುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗೆ ಅದೇ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ಪಡೆಯಲು 13 ಎ ಪ್ರವಾಹದ ಅಗತ್ಯವಿದೆ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ನ ಉದ್ದಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಅತ್ಯಲ್ಪವಾದ ಗಾಳಿಯ ಅಂತರವು ಅಗತ್ಯವಾದ n ಅನ್ನು ಹೆಚ್ಚು ಹೆಚ್ಚಿಸುತ್ತದೆ ಎಂದು ಇದರಿಂದ ನೋಡಬಹುದು. v. ಮತ್ತು ಕಾಯಿಲ್ ಕರೆಂಟ್.

4. ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು F = 72000 Ms ಎಂದು ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. n ನ ಲೆಕ್ಕಾಚಾರದ ಅಗತ್ಯವಿದೆ.s.ಮತ್ತು 800 ತಿರುವುಗಳನ್ನು ಹೊಂದಿರುವ ಪ್ರಾಥಮಿಕ ಅಂಕುಡೊಂಕಾದ ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಪ್ರವಾಹ. ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ಕೋರ್ನಲ್ಲಿ δ = 0.2 ಮಿಮೀ ಅಂತರವಿದೆ. ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ ಕೋರ್ನ ಆಯಾಮಗಳನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 4. ಕೋರ್ S = 2 ∙ 3 ​​= 6 cm2 ನ ಅಡ್ಡ ವಿಭಾಗ (ಈ ಆಕಾರದ ಕೋರ್ಗಳನ್ನು ಹೊಂದಿರುವ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ಗಳನ್ನು ಶಸ್ತ್ರಸಜ್ಜಿತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ).

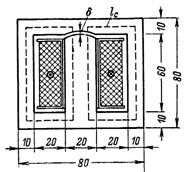
ಅಕ್ಕಿ. 4.

ಕೋರ್ ಮತ್ತು ಗಾಳಿಯ ಅಂತರದ ಇಂಡಕ್ಷನ್ ಬಿ = ಎಫ್ / ಎಸ್ = 72000/6 = 12000 ಜಿ.

B = 12000 G ಗಾಗಿ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ ಸ್ಟೀಲ್ನ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕರ್ವ್ ಪ್ರಕಾರ, ನಾವು ತೀವ್ರತೆಯನ್ನು ನಿರ್ಧರಿಸುತ್ತೇವೆ: Hc = 5 A / cm.

ಉಕ್ಕಿನಲ್ಲಿ ಕಾಂತೀಯ ರೇಖೆಯ ಸರಾಸರಿ ಉದ್ದ lс = 2 ∙ (6 + 3) = 18 ಸೆಂ.

ಗಾಳಿಯ ಅಂತರದಲ್ಲಿ ವೋಲ್ಟೇಜ್ Hδ = 0.8 ∙ B = 9600 A / cm.

ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ ಬಲ I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0.02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0.35 ಎ.

ಶಸ್ತ್ರಸಜ್ಜಿತ ಕೋರ್ನಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎರಡು ಭಾಗಗಳಾಗಿ ವಿಭಜಿಸುತ್ತದೆ, ಇದು ಸೈಡ್ ರಾಡ್ಗಳ ಉದ್ದಕ್ಕೂ ಮುಚ್ಚಲ್ಪಡುತ್ತದೆ, ಅದರ ಅಡ್ಡ ವಿಭಾಗವು S / 2, ಮತ್ತು ಕಾಂತೀಯ ರೇಖೆಯ ಸರಾಸರಿ ಉದ್ದವು lc ಆಗಿದೆ. ಪರಿಣಾಮವಾಗಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಸಾಮಾನ್ಯ ಕೋರ್ ಎಸ್ ಮತ್ತು ವಿದ್ಯುತ್ ಲೈನ್ ಎಲ್ಸಿಯ ಉದ್ದದೊಂದಿಗೆ ಸಾಂಪ್ರದಾಯಿಕ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗೆ ಸಂಪೂರ್ಣವಾಗಿ ಹೋಲುತ್ತದೆ.

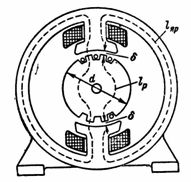
5. DC ಯಂತ್ರದ ಕಾಂತೀಯ ಹರಿವು F = 1280000 Mks. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಎರಕಹೊಯ್ದ ಉಕ್ಕಿನ ನೊಗವನ್ನು ಸರಾಸರಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಲೈನ್ ಉದ್ದದ lа = 80 ಸೆಂ.ಮೀ., ವಿದ್ಯುತ್ ಸ್ಟೀಲ್ ಪ್ಲೇಟ್‌ಗಳಿಂದ ಒಟ್ಟುಗೂಡಿಸಲಾದ ರೋಟರ್ ಅನ್ನು ಸರಾಸರಿ ಕ್ಷೇತ್ರ ಉದ್ದದ ಎಲ್ಆರ್ = 18 ಸೆಂ ಮತ್ತು ಎರಡು ಗಾಳಿಯ ಅಂತರಗಳು δ 0.2 ಸೆಂ.ಮೀ. = 8 ∙ 20 ಸೆಂ 2; ರೋಟರ್ ಮತ್ತು ಪೋಲ್ ವಿಭಾಗ Sр = 12 ∙ 20 cm2... ಲೆಕ್ಕಾಚಾರ n. p. ಮತ್ತು ಪೋಲ್ ಕಾಯಿಲ್ನ ತಿರುವುಗಳ ಸಂಖ್ಯೆ, ಅದರಲ್ಲಿ ಗರಿಷ್ಠ ಮ್ಯಾಗ್ನೆಟೈಸಿಂಗ್ (ಉತ್ತೇಜಕ) ಪ್ರವಾಹವು 1 ಎ (ಚಿತ್ರ 5) ಆಗಿದ್ದರೆ.

ಅಕ್ಕಿ. 5.

ನೊಗ ಮತ್ತು ಧ್ರುವದಲ್ಲಿ ಇಂಡಕ್ಷನ್ Bя = Ф / Sя = 1280000/160 = 8000 G.

Bя = 8000 G ನಲ್ಲಿ ಎರಕಹೊಯ್ದ ಉಕ್ಕಿನ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಕರ್ವ್ ಪ್ರಕಾರ ನೊಗ ಮತ್ತು ಧ್ರುವದಲ್ಲಿನ ವೋಲ್ಟೇಜ್ ಇದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

H = 2.8 A / cm.

ನೊಗದ ವಿಭಾಗದಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟೈಸೇಶನ್ ಬಲವು HЯ ∙ la = 2.8 ∙ 80 = 224 Av.

ರೋಟರ್, ಧ್ರುವ ಮತ್ತು ಗಾಳಿಯ ಅಂತರದಲ್ಲಿ ಇಂಡಕ್ಷನ್ Br = Ф / Ср = 1280000/240 = 5333 ಜಿ.

Br = 5333 Gs Hrp = 0.9 A / cm ನಲ್ಲಿ ಸ್ಟೀಲ್ ಪ್ಲೇಟ್‌ಗಳಿಂದ ಮಾಡಿದ ರೋಟರ್‌ನಲ್ಲಿ ವೋಲ್ಟೇಜ್,

ಮತ್ತು ರೋಟರ್ ವಿಭಾಗದ ಕಾಂತೀಯ ವೋಲ್ಟೇಜ್ Hр ∙ lр = 0.9 ∙ 18 = 16.2 Av.

ಗಾಳಿಯ ಅಂತರದಲ್ಲಿ ವೋಲ್ಟೇಜ್ Hδ = 0.8 ∙ Bδ = 0.8 ∙ 5333 = 4266.4 A / cm.

ಗಾಳಿಯ ಅಂತರದ ಅಡ್ಡ ವಿಭಾಗದಲ್ಲಿ ಕಾಂತೀಯ ವೋಲ್ಟೇಜ್ Hδ ∙ 2 ∙ δ = 4266.4 ∙ 2 ∙ 0.2 = 1706.56 ಎ.

ಸಂಪೂರ್ಣ ಎನ್. c. ಪ್ರತ್ಯೇಕ ವಿಭಾಗಗಳಲ್ಲಿನ ಕಾಂತೀಯ ವೋಲ್ಟೇಜ್ಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16.2 + 1706.56 = 1946.76 Av.

ಎರಡು ಧ್ರುವ ಸುರುಳಿಗಳಲ್ಲಿನ ತಿರುವುಗಳ ಸಂಖ್ಯೆ ω = (I ∙ ω) / I = 1946.76 / 1≈2000.