ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಎಂದರೇನು, ಹಾಪ್ಕಿನ್ಸನ್ ನಿಯಮ

19 ನೇ ಶತಮಾನದ ದ್ವಿತೀಯಾರ್ಧದಲ್ಲಿ, ಇಂಗ್ಲಿಷ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಜಾನ್ ಹಾಪ್ಕಿನ್ಸನ್ ಮತ್ತು ಅವರ ಸಹೋದರ ಎಡ್ವರ್ಡ್ ಹಾಪ್ಕಿನ್ಸನ್, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳ ಸಾಮಾನ್ಯ ಸಿದ್ಧಾಂತವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು, "ಹಾಪ್ಕಿನ್ಸನ್ ಸೂತ್ರ" ಅಥವಾ ಹಾಪ್ಕಿನ್ಸನ್ ನಿಯಮ ಎಂಬ ಗಣಿತದ ಸೂತ್ರವನ್ನು ಪಡೆದರು, ಇದು ಓಮ್ನ ನಿಯಮದ (ಬಳಸಲಾಗಿದೆ) ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ಗಳ ಲೆಕ್ಕಾಚಾರ).

ಆದ್ದರಿಂದ, ಓಮ್ನ ಶಾಸ್ತ್ರೀಯ ನಿಯಮವು ಪ್ರಸ್ತುತ ಮತ್ತು ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ (EMF) ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಗಣಿತೀಯವಾಗಿ ವಿವರಿಸಿದರೆ, ಹಾಪ್ಕಿನ್ಸನ್ ನಿಯಮವು ಕಾಂತೀಯ ಹರಿವು ಮತ್ತು ಕರೆಯಲ್ಪಡುವ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ. ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ (MDF).

ಪರಿಣಾಮವಾಗಿ, ಅದು ಬದಲಾಯಿತು ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಎನ್ನುವುದು ಭೌತಿಕ ಪ್ರಮಾಣವಾಗಿದ್ದು ಅದು ಕಾಂತೀಯ ಹರಿವುಗಳನ್ನು ರಚಿಸಲು ವಿದ್ಯುತ್ ಪ್ರವಾಹಗಳ ಸಾಮರ್ಥ್ಯವನ್ನು ನಿರೂಪಿಸುತ್ತದೆ. ಮತ್ತು ಈ ವಿಷಯದಲ್ಲಿ ಹಾಪ್ಕಿನ್ಸನ್ ಕಾನೂನನ್ನು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳ ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ ಯಶಸ್ವಿಯಾಗಿ ಬಳಸಬಹುದು, ಏಕೆಂದರೆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳಲ್ಲಿನ MDF ಎಲೆಕ್ಟ್ರಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಳಲ್ಲಿ EMF ಗೆ ಹೋಲುತ್ತದೆ. ಹಾಪ್ಕಿನ್ಸನ್ ನಿಯಮದ ಆವಿಷ್ಕಾರದ ದಿನಾಂಕವನ್ನು 1886 ಎಂದು ಪರಿಗಣಿಸಲಾಗಿದೆ.

ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ (MDF) ಯ ಪ್ರಮಾಣವನ್ನು ಆರಂಭದಲ್ಲಿ ಆಂಪಿಯರ್‌ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ ಅಥವಾ ನಾವು ಪ್ರಸ್ತುತ ಅಥವಾ ವಿದ್ಯುತ್ಕಾಂತದೊಂದಿಗೆ ಸುರುಳಿಯ ಬಗ್ಗೆ ಮಾತನಾಡುತ್ತಿದ್ದರೆ, ಲೆಕ್ಕಾಚಾರಗಳ ಅನುಕೂಲಕ್ಕಾಗಿ ಅದರ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಆಂಪಿಯರ್-ತಿರುವುಗಳಲ್ಲಿ ಬಳಸಿ:

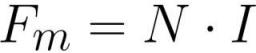
ಅಲ್ಲಿ: Fm ಎಂಬುದು ಸುರುಳಿಯಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಬಲವಾಗಿದೆ [ಆಂಪಿಯರ್ * ತಿರುವು], N ಎಂಬುದು ಸುರುಳಿಯಲ್ಲಿನ ತಿರುವುಗಳ ಸಂಖ್ಯೆ [ತಿರುವು], I ಎಂಬುದು ಸುರುಳಿಯ [ಆಂಪಿಯರ್] ಪ್ರತಿಯೊಂದು ತಿರುವುಗಳಲ್ಲಿನ ಪ್ರವಾಹದ ಪ್ರಮಾಣವಾಗಿದೆ.

ನೀವು ಇಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಮೌಲ್ಯವನ್ನು ನಮೂದಿಸಿದರೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ಗಾಗಿ ಹಾಪ್ಕಿನ್ಸನ್ ನಿಯಮವು ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ:

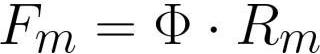
ಅಲ್ಲಿ: Fm ಎಂಬುದು ಸುರುಳಿಯಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಆಗಿದೆ [ಆಂಪಿಯರ್ * ಟರ್ನ್], ಎಫ್ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ [ವೆಬರ್] ಅಥವಾ [ಹೆನ್ರಿ * ಆಂಪಿಯರ್], Rm ಎಂಬುದು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಕಂಡಕ್ಟರ್ [ಆಂಪಿಯರ್ * ಟರ್ನ್ / ವೆಬರ್] ಅಥವಾ [ ತಿರುವು / ಹೆನ್ರಿ] .

ಹಾಪ್ಕಿನ್ಸನ್ ನಿಯಮದ ಪಠ್ಯದ ಸೂತ್ರೀಕರಣವು ಮೂಲತಃ ಈ ಕೆಳಗಿನಂತಿತ್ತು: "ಕವಲೊಡೆದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಬಲಕ್ಕೆ ನೇರವಾಗಿ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ ಮತ್ತು ಒಟ್ಟು ಕಾಂತೀಯ ಪ್ರತಿರೋಧಕ್ಕೆ ವಿಲೋಮ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ." ಅಂದರೆ, ಈ ಕಾನೂನು ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್, ಇಷ್ಟವಿಲ್ಲದಿರುವಿಕೆ ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ನಿರ್ಧರಿಸುತ್ತದೆ:

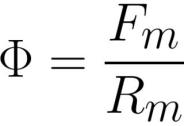
ಇಲ್ಲಿ: F ಎಂಬುದು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ [ವೆಬರ್] ಅಥವಾ [ಹೆನ್ರಿ * ಆಂಪಿಯರ್], Fm ಎಂಬುದು ಸುರುಳಿಯಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ [ಆಂಪಿಯರ್ * ಕ್ರಾಂತಿ], Rm ಎಂಬುದು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಕಂಡಕ್ಟರ್ [ಆಂಪಿಯರ್ * ಕ್ರಾಂತಿ / ವೆಬರ್] ಅಥವಾ [ ತಿರುವು / ಹೆನ್ರಿ] .

ವಾಸ್ತವವಾಗಿ ಮ್ಯಾಗ್ನೆಟೋಮೋಟಿವ್ ಫೋರ್ಸ್ (ಎಮ್‌ಡಿಎಫ್) ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ (ಇಎಮ್‌ಎಫ್) ಗಿಂತ ಮೂಲಭೂತ ವ್ಯತ್ಯಾಸವನ್ನು ಹೊಂದಿದೆ ಎಂಬುದನ್ನು ಇಲ್ಲಿ ಗಮನಿಸುವುದು ಮುಖ್ಯ, ಇದು ಯಾವುದೇ ಕಣಗಳು ನೇರವಾಗಿ ಕಾಂತೀಯ ಹರಿವಿನಲ್ಲಿ ಚಲಿಸುವುದಿಲ್ಲ ಎಂಬ ಅಂಶವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ, ಆದರೆ ಪ್ರವಾಹವು ಕ್ರಿಯೆಯ ಅಡಿಯಲ್ಲಿ ಉದ್ಭವಿಸುತ್ತದೆ. EMF ಚಾರ್ಜ್ಡ್ ಕಣಗಳ ಚಲನೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ, ಉದಾಹರಣೆಗೆ ಲೋಹದ ತಂತಿಗಳಲ್ಲಿನ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು. ಆದಾಗ್ಯೂ, MDS ನ ಕಲ್ಪನೆಯು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ.

ಉದಾಹರಣೆಗೆ, ಒಂದು ಕವಲೊಡೆದ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಪರಿಗಣಿಸಿ, ಇದು ಅಡ್ಡ-ವಿಭಾಗದ ಪ್ರದೇಶದ S ನ ನೊಗವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ, ಅದರ ಉದ್ದಕ್ಕೂ ಒಂದೇ ಆಗಿರುತ್ತದೆ ಮತ್ತು ನೊಗದ ವಸ್ತುವು ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆಯನ್ನು ಹೊಂದಿದೆ.

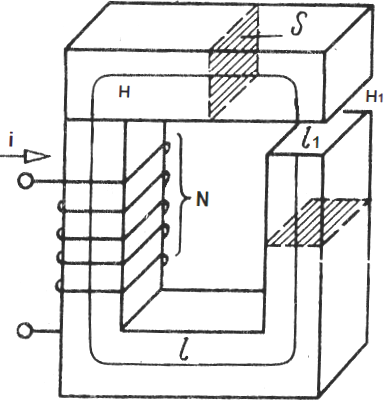
ನೊಗದಲ್ಲಿನ ಅಂತರ - ವಿಭಿನ್ನ ವಸ್ತು, ಕಾಂತೀಯ ಪ್ರವೇಶಸಾಧ್ಯತೆ ಯಾವ mu1. ನೊಗದ ಮೇಲೆ ಇರಿಸಲಾದ ಸುರುಳಿಯು N ತಿರುವುಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಪ್ರಸ್ತುತ i ಸುರುಳಿಯ ಪ್ರತಿಯೊಂದು ತಿರುವುಗಳ ಮೂಲಕ ಹರಿಯುತ್ತದೆ. ನಾವು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಪರಿಚಲನೆ ಪ್ರಮೇಯವನ್ನು ನೊಗದ ಮಧ್ಯಭಾಗಕ್ಕೆ ಅನ್ವಯಿಸುತ್ತೇವೆ:

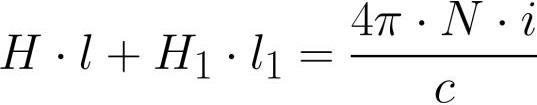
ಅಲ್ಲಿ: H ಎಂಬುದು ನೊಗದೊಳಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ, H1 ಅಂತರದೊಳಗಿನ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ, l ಎಂಬುದು ಯೋಕ್ ಇಂಡಕ್ಷನ್‌ನ ಮಧ್ಯಭಾಗದ ಉದ್ದವಾಗಿದೆ (ಅಂತರವಿಲ್ಲದೆ), l1 ಅಂತರದ ಉದ್ದವಾಗಿದೆ.

ನೊಗದ ಒಳಗೆ ಮತ್ತು ಅಂತರದೊಳಗಿನ ಕಾಂತೀಯ ಹರಿವು ಒಂದೇ ಮೌಲ್ಯವನ್ನು ಹೊಂದಿರುವುದರಿಂದ (ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ರೇಖೆಗಳ ನಿರಂತರತೆಯಿಂದಾಗಿ), Ф = BS ಮತ್ತು В = mu * H ಬರೆದ ನಂತರ, ನಾವು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ಹೆಚ್ಚು ವಿವರವಾಗಿ ಬರೆಯುತ್ತೇವೆ , ಮತ್ತು ಇದನ್ನು ಮೇಲಿನ ಸೂತ್ರಕ್ಕೆ ಬದಲಿಸಿದ ನಂತರ:

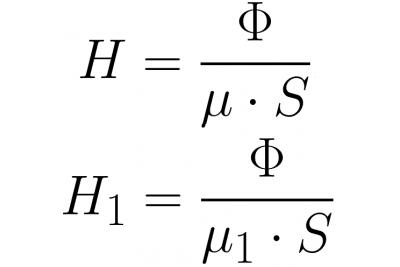
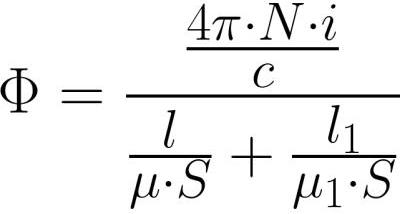
ಎಲೆಕ್ಟ್ರಿಕಲ್ ಸರ್ಕ್ಯೂಟ್‌ಗಳಿಗೆ ಓಮ್‌ನ ಕಾನೂನಿನಲ್ಲಿರುವ ಇಎಮ್‌ಎಫ್‌ನಂತೆ, ಎಂಡಿಎಸ್ ಅನ್ನು ನೋಡುವುದು ಸುಲಭ.

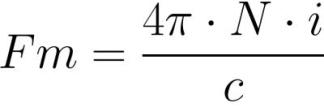
ಇಲ್ಲಿ ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಮತ್ತು ಕಾಂತೀಯ ಪ್ರತಿರೋಧದ ಪಾತ್ರವನ್ನು ವಹಿಸುತ್ತದೆ

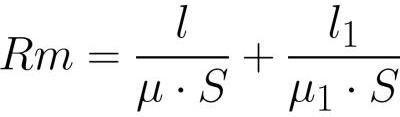
ಪ್ರತಿರೋಧದ ಪಾತ್ರ (ಸಾದೃಶ್ಯದ ಮೂಲಕ ಶಾಸ್ತ್ರೀಯ ಓಮ್ನ ನಿಯಮದೊಂದಿಗೆ).