ಸಂಕ್ಷಿಪ್ತ ಮತ್ತು ಪ್ರವೇಶಿಸಬಹುದಾದ ರೂಪದಲ್ಲಿ ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್‌ನ ಪ್ರಮುಖ ನಿಯಮಗಳು

ಆಧುನಿಕ ಜಗತ್ತಿನಲ್ಲಿ ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್‌ನ ಪ್ರಾಮುಖ್ಯತೆಯು ಪ್ರಾಥಮಿಕವಾಗಿ ದೂರದ ತಂತಿಗಳ ಮೂಲಕ ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಪ್ರಸರಣಕ್ಕೆ ತೆರೆದುಕೊಳ್ಳುವ ವ್ಯಾಪಕ ತಾಂತ್ರಿಕ ಸಾಧ್ಯತೆಗಳೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದೆ, ವಿತರಣೆಯ ವಿಧಾನಗಳಿಗಾಗಿ ಮತ್ತು ವಿದ್ಯುಚ್ಛಕ್ತಿಯನ್ನು ಇತರ ರೂಪಗಳಾಗಿ ಪರಿವರ್ತಿಸಲು, - ಯಾಂತ್ರಿಕ, ಉಷ್ಣ, ಬೆಳಕು, ಇತ್ಯಾದಿ.

ವಿದ್ಯುತ್ ಸ್ಥಾವರಗಳಲ್ಲಿ ಉತ್ಪಾದಿಸಲಾಗುತ್ತದೆ, ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಮೈಲುಗಟ್ಟಲೆ ವಿದ್ಯುತ್ ಲೈನ್‌ಗಳಲ್ಲಿ ಕಳುಹಿಸಲಾಗುತ್ತದೆ - ಮನೆಗಳು ಮತ್ತು ಕೈಗಾರಿಕಾ ಸೌಲಭ್ಯಗಳಿಗೆ, ಅಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಶಕ್ತಿಗಳು ವಿವಿಧ ಉಪಕರಣಗಳು, ಗೃಹೋಪಯೋಗಿ ವಸ್ತುಗಳು, ಬೆಳಕು, ತಾಪನ ಸಾಧನಗಳು ಮತ್ತು ಹೆಚ್ಚಿನ ಮೋಟಾರ್‌ಗಳನ್ನು ಚಾಲನೆ ಮಾಡುತ್ತವೆ. ಒಂದು ಪದದಲ್ಲಿ, ಆಧುನಿಕ ಆರ್ಥಿಕತೆಯನ್ನು ಕಲ್ಪಿಸುವುದು ಅಸಾಧ್ಯ ಮತ್ತು ಗೋಡೆಯ ಮೇಲೆ ಔಟ್ಲೆಟ್ ಇಲ್ಲದೆ ಒಂದೇ ಕೋಣೆಯಲ್ಲ.

ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್ ನಿಯಮಗಳ ಜ್ಞಾನಕ್ಕೆ ಮಾತ್ರ ಇದು ಸಾಧ್ಯವಾಯಿತು, ಇದು ಸಿದ್ಧಾಂತವನ್ನು ವಿದ್ಯುಚ್ಛಕ್ತಿಯ ಪ್ರಾಯೋಗಿಕ ಅನ್ವಯದೊಂದಿಗೆ ಸಂಪರ್ಕಿಸಲು ಅನುವು ಮಾಡಿಕೊಡುತ್ತದೆ. ಈ ಲೇಖನದಲ್ಲಿ, ಈ ನಾಲ್ಕು ಅತ್ಯಂತ ಪ್ರಾಯೋಗಿಕ ಕಾನೂನುಗಳನ್ನು ನಾವು ಹತ್ತಿರದಿಂದ ನೋಡೋಣ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ನಿಯಮ

ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ನಿಯಮವು ವಿದ್ಯುತ್ ಸ್ಥಾವರಗಳಲ್ಲಿ ಸ್ಥಾಪಿಸಲಾದ ಎಲ್ಲಾ ವಿದ್ಯುತ್ ಜನರೇಟರ್ಗಳ ಕಾರ್ಯಾಚರಣೆಯ ಆಧಾರವಾಗಿದೆ, ಮತ್ತು ಮಾತ್ರವಲ್ಲ. ಆದರೆ ಇದು ಕೇವಲ ಗಮನಾರ್ಹವಾದ ಪ್ರವಾಹದಿಂದ ಪ್ರಾರಂಭವಾಯಿತು, 1831 ರಲ್ಲಿ ಮೈಕೆಲ್ ಫ್ಯಾರಡೆ ಅವರು ಸುರುಳಿಗೆ ಸಂಬಂಧಿಸಿದ ವಿದ್ಯುತ್ಕಾಂತದ ಚಲನೆಯ ಪ್ರಯೋಗದಲ್ಲಿ ಕಂಡುಹಿಡಿದರು.

ತನ್ನ ಆವಿಷ್ಕಾರದ ನಿರೀಕ್ಷೆಗಳ ಬಗ್ಗೆ ಫ್ಯಾರಡೆಯನ್ನು ಕೇಳಿದಾಗ, ಅವನು ತನ್ನ ಪ್ರಯೋಗದ ಫಲಿತಾಂಶವನ್ನು ಇನ್ನೂ ಬೆಳೆಯಬೇಕಾದ ಮಗುವಿನ ಜನನಕ್ಕೆ ಹೋಲಿಸಿದನು. ಶೀಘ್ರದಲ್ಲೇ ಈ ನವಜಾತ ಇಡೀ ನಾಗರಿಕ ಪ್ರಪಂಚದ ಮುಖವನ್ನು ಬದಲಿಸಿದ ನಿಜವಾದ ನಾಯಕನಾದನು. ನೋಡಿ - ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ನಿಯಮದ ಪ್ರಾಯೋಗಿಕ ಅಪ್ಲಿಕೇಶನ್

ಜರ್ಮನಿಯ ಐತಿಹಾಸಿಕ ಜಲವಿದ್ಯುತ್ ಸ್ಥಾವರದಲ್ಲಿ ಜನರೇಟರ್

ಆಧುನಿಕ ವಿದ್ಯುತ್ ಸ್ಥಾವರ ಜನರೇಟರ್ ಇದು ಕೇವಲ ಒಂದು ಮ್ಯಾಗ್ನೆಟ್ ಹೊಂದಿರುವ ಸುರುಳಿ ಅಲ್ಲ. ಇದು ಉಕ್ಕಿನ ರಚನೆಗಳು, ನಿರೋಧಕ ತಾಮ್ರದ ಬಸ್‌ಬಾರ್‌ಗಳ ಅನೇಕ ಸುರುಳಿಗಳು, ಟನ್‌ಗಳಷ್ಟು ಕಬ್ಬಿಣ, ಇನ್ಸುಲೇಟಿಂಗ್ ವಸ್ತುಗಳು, ಜೊತೆಗೆ ಮಿಲಿಮೀಟರ್‌ನ ಭಿನ್ನರಾಶಿಗಳವರೆಗೆ ನಿಖರವಾಗಿ ತಯಾರಿಸಲಾದ ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಸಣ್ಣ ಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಬೃಹತ್ ರಚನೆಯಾಗಿದೆ.

ಪ್ರಕೃತಿಯಲ್ಲಿ, ಸಹಜವಾಗಿ, ಅಂತಹ ಸಂಕೀರ್ಣ ಸಾಧನವನ್ನು ಕಂಡುಹಿಡಿಯಲಾಗುವುದಿಲ್ಲ, ಆದರೆ ಪ್ರಯೋಗದಲ್ಲಿ ಪ್ರಕೃತಿಯು ಮನುಷ್ಯನಿಗೆ ಲಭ್ಯವಿರುವ ಬಾಹ್ಯ ಶಕ್ತಿಯ ಪ್ರಭಾವದ ಅಡಿಯಲ್ಲಿ ಯಾಂತ್ರಿಕ ಚಲನೆಗಳ ಮೂಲಕ ವಿದ್ಯುಚ್ಛಕ್ತಿಯನ್ನು ಉತ್ಪಾದಿಸಲು ಸಾಧನವು ಹೇಗೆ ಕೆಲಸ ಮಾಡಬೇಕೆಂದು ತೋರಿಸಿದೆ.

ವಿದ್ಯುತ್ ಸ್ಥಾವರದಲ್ಲಿ ಉತ್ಪತ್ತಿಯಾಗುವ ವಿದ್ಯುತ್ ಅನ್ನು ಪರಿವರ್ತಿಸಲಾಗುತ್ತದೆ, ವಿತರಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಮತ್ತೆ ಪರಿವರ್ತಿಸಲಾಗುತ್ತದೆ ವಿದ್ಯುತ್ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ಗಳು, ಅವರ ಕೆಲಸವು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವಿದ್ಯಮಾನವನ್ನು ಆಧರಿಸಿದೆ, ಕೇವಲ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್, ಜನರೇಟರ್ಗಿಂತ ಭಿನ್ನವಾಗಿ, ಅದರ ವಿನ್ಯಾಸದಲ್ಲಿ ನಿರಂತರವಾಗಿ ಚಲಿಸುವ ಭಾಗಗಳನ್ನು ಒಳಗೊಂಡಿರುವುದಿಲ್ಲ, ಬದಲಿಗೆ ಇದು ಸುರುಳಿಗಳೊಂದಿಗೆ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ಹೊಂದಿರುತ್ತದೆ.

AC ಅಂಕುಡೊಂಕಾದ (ಪ್ರಾಥಮಿಕ ಅಂಕುಡೊಂಕಾದ) ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ ದ್ವಿತೀಯ ವಿಂಡ್ಗಳ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ (ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ದ್ವಿತೀಯಕ ವಿಂಡ್ಗಳು). ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನ ದ್ವಿತೀಯ ವಿಂಡ್ಗಳಿಂದ ವಿದ್ಯುತ್ ಅನ್ನು ಈಗ ಗ್ರಾಹಕರಿಗೆ ವಿತರಿಸಲಾಗುತ್ತದೆ. ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವಿದ್ಯಮಾನ ಮತ್ತು ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್ನ ಅನುಗುಣವಾದ ಕಾನೂನಿನ ಜ್ಞಾನಕ್ಕೆ ಧನ್ಯವಾದಗಳು, ಇದು ಫ್ಯಾರಡೆ ಎಂಬ ಹೆಸರನ್ನು ಹೊಂದಿದೆ.

ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ಕಾನೂನಿನ ಭೌತಿಕ ಅರ್ಥವು ಕಾಲಾನಂತರದಲ್ಲಿ ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಬದಲಾದಾಗ ಎಡ್ಡಿ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ನೋಟವಾಗಿದೆ, ಇದು ಕೆಲಸ ಮಾಡುವ ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ನಲ್ಲಿ ನಿಖರವಾಗಿ ಸಂಭವಿಸುತ್ತದೆ.

ಪ್ರಾಯೋಗಿಕವಾಗಿ, ವಾಹಕದಿಂದ ಸುತ್ತುವರಿದ ಮೇಲ್ಮೈಯನ್ನು ಭೇದಿಸುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಬದಲಾದಾಗ, ಕಂಡಕ್ಟರ್‌ನಲ್ಲಿ ಇಎಮ್‌ಎಫ್ ಅನ್ನು ಪ್ರಚೋದಿಸಲಾಗುತ್ತದೆ, ಅದರ ಮೌಲ್ಯವು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ (ಎಫ್) ನ ಬದಲಾವಣೆಯ ದರಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದರೆ ಪ್ರಚೋದಿತ ಇಎಮ್‌ಎಫ್‌ನ ಚಿಹ್ನೆ ಮಾಡಿದ ಬದಲಾವಣೆಯ ದರಕ್ಕೆ ವಿರುದ್ಧವಾಗಿದೆ F. ಈ ಸಂಬಂಧವನ್ನು "ಫ್ಲೋ ನಿಯಮ" ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ:

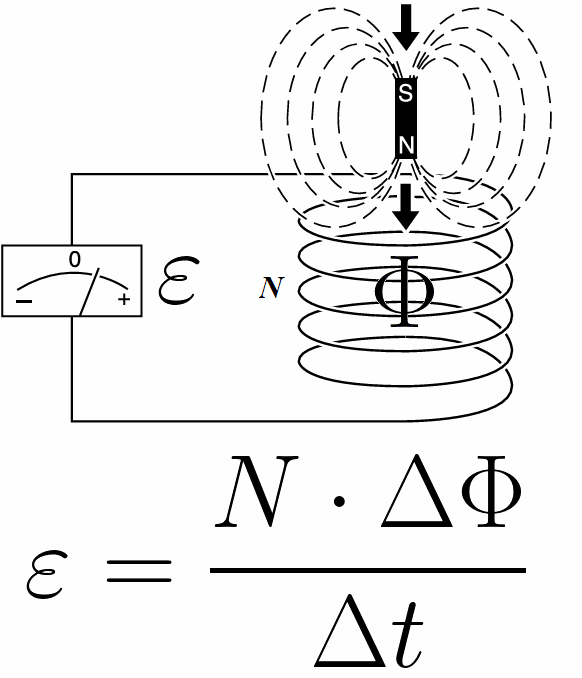
ಲೂಪ್ ಅನ್ನು ಭೇದಿಸುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ನೇರವಾಗಿ ಬದಲಾಯಿಸುವುದರ ಜೊತೆಗೆ, ಅದರಲ್ಲಿ EMF ಅನ್ನು ಪಡೆಯುವ ಮತ್ತೊಂದು ವಿಧಾನವು ಸಾಧ್ಯ, - ಲೊರೆಂಟ್ಜ್ ಬಲವನ್ನು ಬಳಸುವುದು.

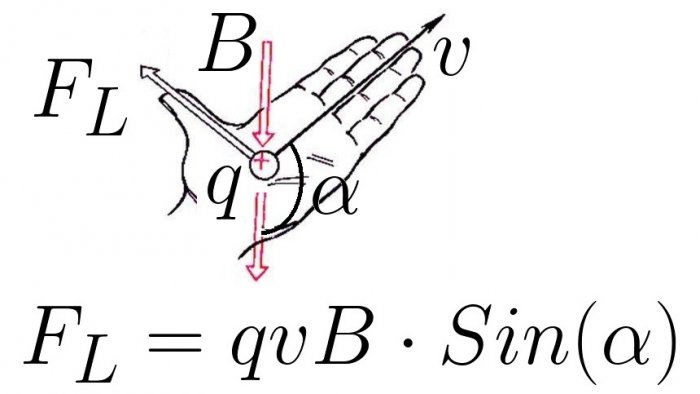
ಲೊರೆಂಟ್ಜ್ ಬಲದ ಪ್ರಮಾಣವು ನಿಮಗೆ ತಿಳಿದಿರುವಂತೆ, ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಚಾರ್ಜ್ನ ಚಲನೆಯ ವೇಗವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ, ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್ನ ಪ್ರಮಾಣ ಮತ್ತು ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ಗೆ ಹೋಲಿಸಿದರೆ ನಿರ್ದಿಷ್ಟ ಚಾರ್ಜ್ ಚಲಿಸುವ ಕೋನದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ:

ಧನಾತ್ಮಕ ಆವೇಶಕ್ಕಾಗಿ ಲೊರೆಂಟ್ಜ್ ಬಲದ ದಿಕ್ಕನ್ನು "ಎಡ-ಕೈ" ನಿಯಮದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ: ನಿಮ್ಮ ಎಡಗೈಯನ್ನು ನೀವು ಇರಿಸಿದರೆ ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ ವೆಕ್ಟರ್ ಅಂಗೈಗೆ ಪ್ರವೇಶಿಸುತ್ತದೆ ಮತ್ತು ನಾಲ್ಕು ಚಾಚಿದ ಬೆರಳುಗಳನ್ನು ಚಲನೆಯ ದಿಕ್ಕಿನಲ್ಲಿ ಇರಿಸಲಾಗುತ್ತದೆ. ಧನಾತ್ಮಕ ಆವೇಶ, ನಂತರ 90 ಡಿಗ್ರಿಗಳಲ್ಲಿ ಹೆಬ್ಬೆರಳು ಬಾಗಿದ ಲೊರೆಂಟ್ಜ್ ಬಲದ ದಿಕ್ಕನ್ನು ಸೂಚಿಸುತ್ತದೆ.

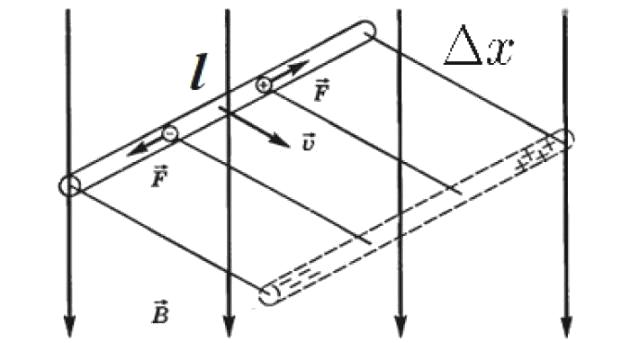
ಅಂತಹ ಪ್ರಕರಣದ ಸರಳ ಉದಾಹರಣೆಯನ್ನು ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. ಇಲ್ಲಿ, ಲೋರೆಂಟ್ಜ್ ಬಲವು ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ಚಲಿಸುವ ಕಂಡಕ್ಟರ್‌ನ ಮೇಲಿನ ತುದಿಯನ್ನು (ತಾಮ್ರದ ತಂತಿಯ ತುಂಡು) ಧನಾತ್ಮಕವಾಗಿ ಚಾರ್ಜ್ ಮಾಡಲು ಕಾರಣವಾಗುತ್ತದೆ ಮತ್ತು ಅದರ ಕೆಳಗಿನ ತುದಿಯು ಋಣಾತ್ಮಕವಾಗಿ ಚಾರ್ಜ್ ಆಗುತ್ತದೆ, ಏಕೆಂದರೆ ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಋಣಾತ್ಮಕ ಆವೇಶವನ್ನು ಹೊಂದಿರುತ್ತವೆ ಮತ್ತು ಅವುಗಳು ಇಲ್ಲಿಗೆ ಚಲಿಸುತ್ತವೆ. .

ಎಲೆಕ್ಟ್ರಾನ್‌ಗಳು ಅವುಗಳ ನಡುವಿನ ಕೂಲಂಬ್ ಆಕರ್ಷಣೆ ಮತ್ತು ತಂತಿಯ ಎದುರು ಭಾಗದಲ್ಲಿರುವ ಧನಾತ್ಮಕ ಆವೇಶವು ಲೊರೆಂಟ್ಜ್ ಬಲವನ್ನು ಸಮತೋಲನಗೊಳಿಸುವವರೆಗೆ ಕೆಳಕ್ಕೆ ಚಲಿಸುತ್ತದೆ.

ಈ ಪ್ರಕ್ರಿಯೆಯು ಕಂಡಕ್ಟರ್ನಲ್ಲಿ ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ನ ನೋಟವನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ ಮತ್ತು ಅದು ಬದಲಾದಂತೆ, ನೇರವಾಗಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ನಿಯಮಕ್ಕೆ ಸಂಬಂಧಿಸಿದೆ. ವಾಸ್ತವವಾಗಿ, ತಂತಿಯಲ್ಲಿನ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿ E ಅನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಕಾಣಬಹುದು (ತಂತಿಯು ವೆಕ್ಟರ್ B ಗೆ ಲಂಬ ಕೋನಗಳಲ್ಲಿ ಚಲಿಸುತ್ತದೆ ಎಂದು ಊಹಿಸಿ):

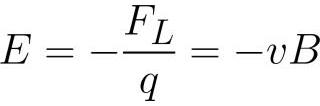
ಆದ್ದರಿಂದ, ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ ಅನ್ನು ಈ ಕೆಳಗಿನಂತೆ ವ್ಯಕ್ತಪಡಿಸಬಹುದು:

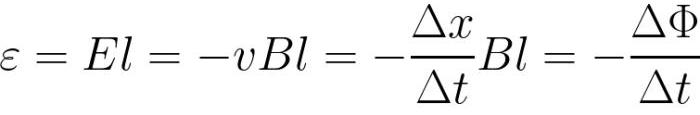
ನೀಡಿರುವ ಉದಾಹರಣೆಯಲ್ಲಿ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಎಫ್ ಸ್ವತಃ (ಒಂದು ವಸ್ತುವಾಗಿ) ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಬದಲಾವಣೆಗಳಿಗೆ ಒಳಗಾಗುವುದಿಲ್ಲ ಎಂದು ಗಮನಿಸಬಹುದು, ಆದರೆ ತಂತಿಯು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಇರುವ ಪ್ರದೇಶವನ್ನು ದಾಟುತ್ತದೆ ಮತ್ತು ತಂತಿಯು ಹಾದುಹೋಗುವ ಪ್ರದೇಶವನ್ನು ನೀವು ಸುಲಭವಾಗಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡಬಹುದು. ನಿರ್ದಿಷ್ಟ ಸಮಯದಲ್ಲಿ ಆ ಜಾಗದ ಮೂಲಕ ಚಲಿಸುವ ಮೂಲಕ (ಅಂದರೆ ಮೇಲೆ ತಿಳಿಸಿದ ಕಾಂತೀಯ ಹರಿವಿನ ಬದಲಾವಣೆಯ ದರ).

ಸಾಮಾನ್ಯ ಸಂದರ್ಭದಲ್ಲಿ, "ಫ್ಲಕ್ಸ್ ನಿಯಮ" ದ ಪ್ರಕಾರ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿನ ಇಎಮ್‌ಎಫ್ ಆ ಸರ್ಕ್ಯೂಟ್ ಮೂಲಕ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್‌ನ ಬದಲಾವಣೆಯ ದರಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಎಂದು ತೀರ್ಮಾನಿಸಲು ನಾವು ಅರ್ಹರಾಗಿದ್ದೇವೆ, ಇದರ ಮೌಲ್ಯವನ್ನು ಲೆಕ್ಕಿಸದೆ ವಿರುದ್ಧ ಚಿಹ್ನೆಯೊಂದಿಗೆ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಸ್ಥಳಾಂತರದ ಪರಿಣಾಮವಾಗಿ (ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ದಾಟುವುದು) ಅಥವಾ ಲೂಪ್ ಅಥವಾ ಎರಡರ ವಿರೂಪತೆಯ ಪರಿಣಾಮವಾಗಿ ಸ್ಥಿರ ಲೂಪ್‌ನಲ್ಲಿ ಸಮಯದೊಂದಿಗೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್‌ನಲ್ಲಿನ ಬದಲಾವಣೆಯಿಂದಾಗಿ ಫ್ಲಕ್ಸ್ ಎಫ್ ನೇರವಾಗಿ ಬದಲಾಗುತ್ತದೆ.

ಆಂಪಿಯರ್ ಕಾನೂನು

ವಿದ್ಯುತ್ ಸ್ಥಾವರಗಳಲ್ಲಿ ಉತ್ಪತ್ತಿಯಾಗುವ ಶಕ್ತಿಯ ಗಮನಾರ್ಹ ಭಾಗವನ್ನು ಉದ್ಯಮಗಳಿಗೆ ಕಳುಹಿಸಲಾಗುತ್ತದೆ, ಅಲ್ಲಿ ವಿವಿಧ ಲೋಹದ ಕತ್ತರಿಸುವ ಯಂತ್ರಗಳ ಎಂಜಿನ್ಗಳನ್ನು ವಿದ್ಯುತ್ ಸರಬರಾಜು ಮಾಡಲಾಗುತ್ತದೆ. ಎಲೆಕ್ಟ್ರಿಕ್ ಮೋಟಾರ್ಗಳ ಕಾರ್ಯಾಚರಣೆಯು ಅವರ ವಿನ್ಯಾಸಕರ ತಿಳುವಳಿಕೆಯನ್ನು ಆಧರಿಸಿದೆ ಆಂಪಿಯರ್ ಕಾನೂನು.

ಈ ಕಾನೂನನ್ನು ಆಂಡ್ರೆ ಮೇರಿ ಆಂಪಿಯರ್ ಅವರು 1820 ರಲ್ಲಿ ನೇರ ಪ್ರವಾಹಗಳಿಗಾಗಿ ರಚಿಸಿದರು (ಈ ಕಾನೂನನ್ನು ವಿದ್ಯುತ್ ಪ್ರವಾಹಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ನಿಯಮ ಎಂದೂ ಕರೆಯುವುದು ಕಾಕತಾಳೀಯವಲ್ಲ).

ಆಂಪಿಯರ್‌ನ ನಿಯಮದ ಪ್ರಕಾರ, ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಪ್ರವಾಹಗಳನ್ನು ಹೊಂದಿರುವ ಸಮಾನಾಂತರ ತಂತಿಗಳು ಪರಸ್ಪರ ಆಕರ್ಷಿಸುತ್ತವೆ ಮತ್ತು ವಿರುದ್ಧವಾಗಿ ನಿರ್ದೇಶಿಸಿದ ಪ್ರವಾಹಗಳೊಂದಿಗೆ ಸಮಾನಾಂತರ ತಂತಿಗಳು ಪರಸ್ಪರ ಹಿಮ್ಮೆಟ್ಟಿಸುತ್ತವೆ. ಹೆಚ್ಚುವರಿಯಾಗಿ, ಆಂಪಿಯರ್ ನಿಯಮವು ಒಂದು ನಿರ್ದಿಷ್ಟ ಕ್ಷೇತ್ರದಲ್ಲಿ ಪ್ರಸ್ತುತ-ಸಾಗಿಸುವ ವಾಹಕದ ಮೇಲೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವನ್ನು ನಿರ್ಧರಿಸಲು ಹೆಬ್ಬೆರಳಿನ ನಿಯಮವನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಸರಳ ರೂಪದಲ್ಲಿ, ಆಂಪಿಯರ್ನ ನಿಯಮವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಹೇಳಬಹುದು: ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ವಿದ್ಯುತ್-ವಾಹಕದ ಅಂಶದ ಮೇಲೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವು (ಆಂಪಿಯರ್ನ ಬಲ ಎಂದು ಕರೆಯಲ್ಪಡುತ್ತದೆ) ವಾಹಕದಲ್ಲಿನ ಪ್ರವಾಹದ ಪ್ರಮಾಣಕ್ಕೆ ನೇರವಾಗಿ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. ಮತ್ತು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ಮೌಲ್ಯದಿಂದ ತಂತಿಯ ಉದ್ದದ ಅಂಶದ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ.

ಅಂತೆಯೇ, ಆಂಪಿಯರ್ ಬಲದ ಮಾಡ್ಯುಲಸ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವ ಅಭಿವ್ಯಕ್ತಿಯು ಈ ಬಲವು ಕಾರ್ಯನಿರ್ವಹಿಸುವ ವಾಹಕದಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ ವೆಕ್ಟರ್ ಮತ್ತು ಪ್ರಸ್ತುತ ವೆಕ್ಟರ್ ನಡುವಿನ ಕೋನದ ಸೈನ್ ಅನ್ನು ಹೊಂದಿರುತ್ತದೆ (ಆಂಪಿಯರ್ನ ಬಲದ ದಿಕ್ಕನ್ನು ನಿರ್ಧರಿಸಲು, ನೀವು ಎಡಗೈ ನಿಯಮವನ್ನು ಬಳಸಬಹುದು. ):

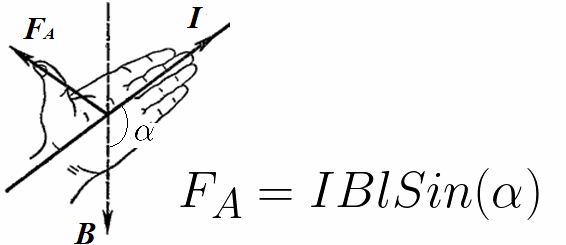
ಎರಡು ಪರಸ್ಪರ ವಾಹಕಗಳಿಗೆ ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ, ಆಂಪಿಯರ್ನ ಬಲವು ಆ ವಾಹಕಗಳಲ್ಲಿನ ಪ್ರವಾಹಗಳ ಆಯಾ ದಿಕ್ಕುಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾದ ದಿಕ್ಕಿನಲ್ಲಿ ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದರ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.

I1 ಮತ್ತು I2 ಪ್ರವಾಹಗಳೊಂದಿಗೆ ನಿರ್ವಾತದಲ್ಲಿ ಎರಡು ಅನಂತ ಉದ್ದವಾದ ತೆಳುವಾದ ವಾಹಕಗಳಿವೆ ಎಂದು ಭಾವಿಸೋಣ ಮತ್ತು ಎಲ್ಲೆಡೆ ವಾಹಕಗಳ ನಡುವಿನ ಅಂತರವು r ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.ತಂತಿಯ ಯುನಿಟ್ ಉದ್ದದ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಆಂಪಿಯರ್ ಬಲವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅವಶ್ಯಕ (ಉದಾಹರಣೆಗೆ, ಎರಡನೆಯ ಬದಿಯಲ್ಲಿರುವ ಮೊದಲ ತಂತಿಯಲ್ಲಿ).

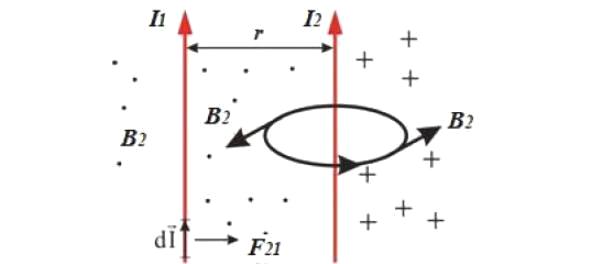
ಬಯೋ-ಸಾವರ್ಟ್-ಲ್ಯಾಪ್ಲೇಸ್ ಕಾನೂನಿನ ಪ್ರಕಾರ, ಪ್ರಸ್ತುತ I2 ನೊಂದಿಗೆ ಅನಂತ ವಾಹಕದಿಂದ r ದೂರದಲ್ಲಿ, ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಇಂಡಕ್ಷನ್ ಅನ್ನು ಹೊಂದಿರುತ್ತದೆ:

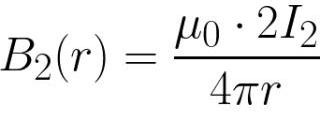
ಈಗ ನೀವು ಆಂಪಿಯರ್ ಬಲವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು ಅದು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ (ನೀಡಿದ ಇಂಡಕ್ಷನ್ ಹೊಂದಿರುವ ಸ್ಥಳದಲ್ಲಿ) ಇರುವ ಮೊದಲ ತಂತಿಯ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ:

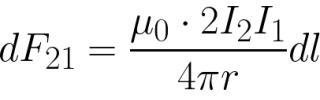
ಉದ್ದದ ಮೇಲೆ ಈ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಸಂಯೋಜಿಸಿ, ತದನಂತರ ಉದ್ದಕ್ಕೆ ಒಂದನ್ನು ಬದಲಿಸಿ, ಎರಡನೆಯ ಬದಿಯಲ್ಲಿರುವ ಮೊದಲ ತಂತಿಯ ಪ್ರತಿ ಯುನಿಟ್ ಉದ್ದಕ್ಕೆ ಆಂಪಿಯರ್-ಫೋರ್ಸ್ ನಟನೆಯನ್ನು ನಾವು ಪಡೆಯುತ್ತೇವೆ. ಇದೇ ರೀತಿಯ ಶಕ್ತಿ, ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಮಾತ್ರ, ಮೊದಲನೆಯ ಬದಿಯಿಂದ ಎರಡನೇ ತಂತಿಯ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ.

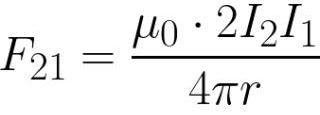
ಆಂಪಿಯರ್ ಕಾನೂನಿನ ತಿಳುವಳಿಕೆಯಿಲ್ಲದೆ, ಕನಿಷ್ಠ ಒಂದು ಸಾಮಾನ್ಯ ವಿದ್ಯುತ್ ಮೋಟರ್ ಅನ್ನು ಗುಣಾತ್ಮಕವಾಗಿ ವಿನ್ಯಾಸಗೊಳಿಸಲು ಮತ್ತು ಜೋಡಿಸಲು ಅಸಾಧ್ಯವಾಗಿದೆ.

ವಿದ್ಯುತ್ ಮೋಟರ್ನ ಕಾರ್ಯಾಚರಣೆ ಮತ್ತು ವಿನ್ಯಾಸದ ತತ್ವ

ಅಸಮಕಾಲಿಕ ವಿದ್ಯುತ್ ಮೋಟರ್ಗಳ ವಿಧಗಳು, ಅವುಗಳ ಗುಣಲಕ್ಷಣಗಳು

ಜೌಲ್-ಲೆನ್ಜ್ ಕಾನೂನು

ಎಲ್ಲಾ ವಿದ್ಯುತ್ ಶಕ್ತಿ ಪ್ರಸರಣ ಮಾರ್ಗ, ಈ ತಂತಿಗಳು ಬಿಸಿಯಾಗಲು ಕಾರಣವಾಗುತ್ತದೆ. ಇದರ ಜೊತೆಯಲ್ಲಿ, ಗಮನಾರ್ಹವಾದ ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ವಿವಿಧ ತಾಪನ ಸಾಧನಗಳನ್ನು ಶಕ್ತಿಯುತಗೊಳಿಸಲು, ಟಂಗ್ಸ್ಟನ್ ಫಿಲಾಮೆಂಟ್ಸ್ ಅನ್ನು ಹೆಚ್ಚಿನ ತಾಪಮಾನಕ್ಕೆ ಬಿಸಿಮಾಡಲು ಉದ್ದೇಶಿಸಿ ಬಳಸಲಾಗುತ್ತದೆ. ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ತಾಪನ ಪರಿಣಾಮದ ಲೆಕ್ಕಾಚಾರಗಳು ಜೌಲ್-ಲೆನ್ಜ್ ನಿಯಮವನ್ನು ಆಧರಿಸಿವೆ, ಇದನ್ನು 1841 ರಲ್ಲಿ ಜೇಮ್ಸ್ ಜೌಲ್ ಮತ್ತು ಸ್ವತಂತ್ರವಾಗಿ 1842 ರಲ್ಲಿ ಎಮಿಲ್ ಲೆನ್ಜ್ ಕಂಡುಹಿಡಿದರು.

ಈ ಕಾನೂನು ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಉಷ್ಣ ಪರಿಣಾಮವನ್ನು ಅಳೆಯುತ್ತದೆ.ಇದನ್ನು ಈ ಕೆಳಗಿನಂತೆ ರೂಪಿಸಲಾಗಿದೆ: "ನೇರ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಅದರಲ್ಲಿ ಹರಿಯುವಾಗ ಮಾಧ್ಯಮದ ಯುನಿಟ್ ಪರಿಮಾಣಕ್ಕೆ (w) ಬಿಡುಗಡೆಯಾದ ಶಾಖದ ಶಕ್ತಿಯು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ಮೌಲ್ಯದಿಂದ ವಿದ್ಯುತ್ ಪ್ರವಾಹ ಸಾಂದ್ರತೆಯ (j) ಉತ್ಪನ್ನಕ್ಕೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. (ಇ) ".

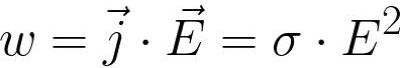
ತೆಳುವಾದ ತಂತಿಗಳಿಗೆ, ಕಾನೂನಿನ ಅವಿಭಾಜ್ಯ ರೂಪವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ: "ಸರ್ಕ್ಯೂಟ್ನ ಒಂದು ವಿಭಾಗದಿಂದ ಪ್ರತಿ ಯುನಿಟ್ ಸಮಯಕ್ಕೆ ಬಿಡುಗಡೆಯಾಗುವ ಶಾಖದ ಪ್ರಮಾಣವು ವಿಭಾಗದ ಪ್ರತಿರೋಧದಿಂದ ಪರಿಗಣಿಸಲಾದ ವಿಭಾಗದಲ್ಲಿನ ಪ್ರಸ್ತುತದ ವರ್ಗದ ಉತ್ಪನ್ನಕ್ಕೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. » ಇದನ್ನು ಈ ಕೆಳಗಿನ ರೂಪದಲ್ಲಿ ಬರೆಯಲಾಗಿದೆ:

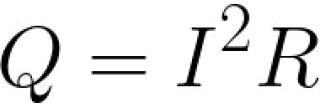
ಜೌಲ್-ಲೆನ್ಜ್ ಕಾನೂನು ದೂರದ ತಂತಿಗಳ ಮೇಲೆ ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಪ್ರಸರಣದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಪ್ರಾಯೋಗಿಕ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಹೊಂದಿದೆ.

ವಿದ್ಯುತ್ ಲೈನ್ನಲ್ಲಿನ ಪ್ರಸ್ತುತದ ಉಷ್ಣ ಪರಿಣಾಮವು ಅನಪೇಕ್ಷಿತವಾಗಿದೆ ಏಕೆಂದರೆ ಇದು ಶಕ್ತಿಯ ನಷ್ಟಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ ಎಂದು ತೀರ್ಮಾನವಾಗಿದೆ. ಮತ್ತು ಪ್ರಸರಣ ಶಕ್ತಿಯು ವೋಲ್ಟೇಜ್ ಮತ್ತು ಪ್ರವಾಹದ ಪ್ರಮಾಣ ಎರಡನ್ನೂ ರೇಖಾತ್ಮಕವಾಗಿ ಅವಲಂಬಿಸಿರುವುದರಿಂದ, ತಾಪನ ಶಕ್ತಿಯು ಪ್ರಸ್ತುತದ ವರ್ಗಕ್ಕೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ, ವಿದ್ಯುತ್ ಪ್ರಸರಣಗೊಳ್ಳುವ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಹೆಚ್ಚಿಸಲು ಅನುಕೂಲಕರವಾಗಿದೆ, ಅದಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಪ್ರಸ್ತುತವನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ.

ಓಮ್ನ ಕಾನೂನು

ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನ ಮೂಲ ನಿಯಮ - ಓಮ್ಸ್ ನಿಯಮವನ್ನು ಜಾರ್ಜ್ ಓಮ್ 1826 ರಲ್ಲಿ ಕಂಡುಹಿಡಿದನು.… ತಂತಿಯ ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧ ಅಥವಾ ವಾಹಕತೆಯನ್ನು (ವಿದ್ಯುತ್ ವಾಹಕತೆ) ಅವಲಂಬಿಸಿ ವಿದ್ಯುತ್ ವೋಲ್ಟೇಜ್ ಮತ್ತು ಪ್ರವಾಹದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಕಾನೂನು ನಿರ್ಧರಿಸುತ್ತದೆ. ಆಧುನಿಕ ಪರಿಭಾಷೆಯಲ್ಲಿ, ಸಂಪೂರ್ಣ ಸರ್ಕ್ಯೂಟ್ಗಾಗಿ ಓಮ್ನ ನಿಯಮವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಬರೆಯಲಾಗಿದೆ:

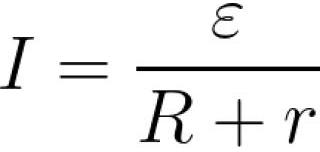
ಆರ್ - ಮೂಲ ಆಂತರಿಕ ಪ್ರತಿರೋಧ, ಆರ್ - ಲೋಡ್ ಪ್ರತಿರೋಧ, ಇ - ಮೂಲ ಇಎಮ್ಎಫ್, ಐ - ಸರ್ಕ್ಯೂಟ್ ಕರೆಂಟ್

ಈ ದಾಖಲೆಯಿಂದ ಅದು ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿನ ಇಎಮ್‌ಎಫ್ ಅನ್ನು ಅನುಸರಿಸುತ್ತದೆ, ಅದರ ಮೂಲಕ ಮೂಲದಿಂದ ನೀಡಲಾದ ಪ್ರವಾಹವು ಇದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

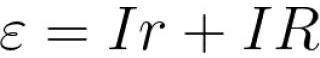
ಇದರರ್ಥ ಮುಚ್ಚಿದ ಸರ್ಕ್ಯೂಟ್ಗಾಗಿ, ಮೂಲ ಇಎಮ್ಎಫ್ ಬಾಹ್ಯ ಸರ್ಕ್ಯೂಟ್ನ ವೋಲ್ಟೇಜ್ ಡ್ರಾಪ್ ಮತ್ತು ಮೂಲದ ಆಂತರಿಕ ಪ್ರತಿರೋಧದ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಓಮ್ನ ನಿಯಮವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ರೂಪಿಸಲಾಗಿದೆ: "ಸರ್ಕ್ಯೂಟ್ನ ಒಂದು ವಿಭಾಗದಲ್ಲಿನ ಪ್ರವಾಹವು ಅದರ ತುದಿಗಳಲ್ಲಿನ ವೋಲ್ಟೇಜ್ಗೆ ನೇರವಾಗಿ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ ಮತ್ತು ಸರ್ಕ್ಯೂಟ್ನ ಈ ವಿಭಾಗದ ವಿದ್ಯುತ್ ಪ್ರತಿರೋಧಕ್ಕೆ ವಿಲೋಮ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ." ಓಮ್ನ ನಿಯಮದ ಮತ್ತೊಂದು ಸಂಕೇತವೆಂದರೆ ವಾಹಕತೆ ಜಿ (ವಿದ್ಯುತ್ ವಾಹಕತೆ):

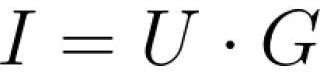
ಸರ್ಕ್ಯೂಟ್ನ ಒಂದು ವಿಭಾಗಕ್ಕೆ ಓಮ್ನ ನಿಯಮ

ಆಚರಣೆಯಲ್ಲಿ ಓಮ್ನ ನಿಯಮದ ಅನ್ವಯ

ವೋಲ್ಟೇಜ್, ಕರೆಂಟ್, ರೆಸಿಸ್ಟೆನ್ಸ್ ಎಂದರೇನು ಮತ್ತು ಅವುಗಳನ್ನು ಆಚರಣೆಯಲ್ಲಿ ಹೇಗೆ ಬಳಸಲಾಗುತ್ತದೆ